Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 5.Problemas - Ex. 233

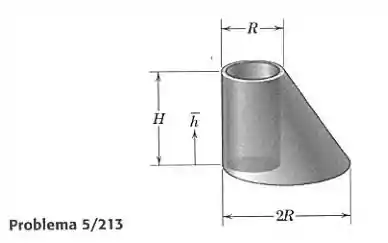
O corpo homogêneo mostrado é constituído a partir do corpo sólido do Prob. 5/211 e, a seguir, removendo um volume cilíndrico com um diâmetro pouco menor que R , como mostrado, deixando uma parede fina na parte esquerda do corpo, bem como no seu topo. Determine a altura h - de seu centro de massa, acima da base do corpo.

Passo 1

Do Prob. 5/211, sabemos que o volume do sóllido sem removermos o cilindro era

V 1 = 7 3 π R 2 H

E que seu centro de massa fica a uma altura

h - 1 = 11 28 H

Se combinarmos o sólido completo com o buraco do cilindro, com volume considerado negativo, conseguimos calcular a altura do centro de massa com a seguinte fórmula:

h - = V 1 h - 1 - V 2 h - 2 V 1 - V 2

Passo 2

É claro que a altura do centro de massa do cilindro vai ser a metade da altura total:

h - 2 = H 2

O volume é dado por:

V 2 = π R 2 H

Então substituindo na fórmula:

h - = V 1 h - 1 - V 2 h - 2 V 1 - V 2 = 7 3 π R 2 H ⋅ 11 28 H - π R H 2 ⋅ H 2 7 3 π R 2 H - π R 2 H = 11 12 π R 2 H 2 - 6 12 π R 2 H 2 7 3 π R 2 H - 3 3 π R 2 H

= 5 12 π R 2 H 2 4 3 π R 2 H = 5 12 ⋅ 3 4 H = 5 16 H

Resposta

h - = 5 16 H

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

20- Deixe que e → ∞ e determine as coordenadas x e y do centroide da área sombreada.
23- Use os resultados do Exemplo 5/3 para calcular as coordenadas do centro de massa da parte mostrada do cilindro sólido homogêneo.
22- Determine a coordenada y do centroide da área sombreada.
24- Determine as coordenadas do centroide da área sombreada
25- Determine as coordenadas x e y do centroide da área sombreada.