Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 35

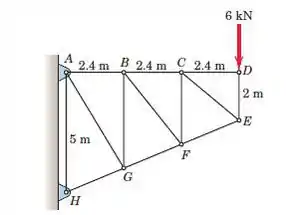
Calcule as forças nos membros AB, BG e GF. Resolva para cada força a partir de uma equação de equilíbrio que contém essa força como a única incógnita.

Passo 1

Primeiro, vamos dar uma olhada em alguma geometria. Podemos ver que, como AB = BC = CDCF é 3m e BG é 4 m. Em seguida, puxe o formulário horizontal E para CF. Obtemos um triângulo retângulo e sua hipotenusa é de 2,6m. Se repetirmos isso para os pontos F e G, veremos que todos esses triângulos são semelhantes.

Passo 2

Cortamos AB, BG e GF. Esta seção cortada deve estar em equilíbrio. Primeiro, vejamos o momento sobre B de todas as forças externas (agora as forças AB. BG e GF agem como forças externas).

6 k N ⋅ 4.8 m = G F 2.4 m ⋅ 1 2.6 + 3 m ⋅ 2.4 2.6

G F = 7.8 k N

Em seguida, a partir do momento sobre C, podemos obter BG.

6 k N ⋅ 2.4 m + B G ⋅ 2.4 m = F G ⋅ 3 m ⋅ 2.4 2.6

B G = 3 k N

Por fim, olhe o momento sobre F para obter AB.

6 k N ⋅ 2.4 m + B G ⋅ 2.4 m = A B ⋅ 3 m

A B = 7.2 k N

Resposta

G F = 7.8 k N B G = 3 k N A B = 7.2 k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A treliça da tabuleta é projetada para suportar uma carga de vento horizontal de 800 lb. Se a resultante dessa carga passar pelo ponto C, calcule as forças nos membros BG e BF.
A treliça é composta por triângulos equiláteros e suporta a carga L. Determine as forças nas barras CG e GF. Identifique aqueles membros para os quais as equações de equilíbrio não são suficientes par
Determine a força no membro DG para a treliça em termos de carga L. Todos os ângulos internos são 60 ° .
A treliça mostrada é composta por 45 ∘ triângulos retângulos. Os membros cruzados nos dois painéis centrais são tirantes delgados, incapazes de suportar compressão. Retenha as duas hastes que estão so
Os quadros articulados ACE e DFB são conectados por duas barras articuladas, AB e CD, que se cruzam sem serem conectadas. Calcule a força em AB.