Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas - Ex. 150
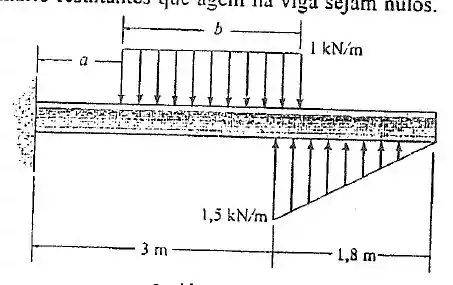
150. A viga está sujeita ao carregamento distribuído. Determine o comprimento do carregamento uniforme e sua posição sobre a viga de modo que a força e o momento de binário resultantes que agem na viga sejam nulos.
Passo 1
Oi, querido! Queremos encontrar e para que na viga
O esquema para resolver esse problema é primeiro calcularmos a intensidade da força e o ponto ela atua na parte de baixo, porque é onde temos detalhes do que está acontecendo, aí depois aplicamos as condições que o enunciado fornece, para aí sim acharmos o que ele quer.
A intensidade da força é igual a área total sob o diagrama de carregamento, isso vale para as duas partes que temos na figura.
A posição do centroide em relação ao próprio diagrama, que é onde essa força atua é dada por uma integral, mas para figuras geométricas mais simples, como o nosso caso, tem fórmulas tabeladas que você pode encontrar no apêndice C na seção C.4.
Passo 2
Pelo o que foi dito no passo 1, vamos achar a intensidade da força da parte inferior através da área do triangulo formado, então:
Onde é base do triângulo e é a altura do triângulo, (isso pode ser constatado na imagem que o livro fornece).
O centroide do triangulo é encontrado na posição:
Essa posição em relação ao próprio diagrama, agora em relação a parede na extremidade esquerda da viga
Passo 3
O mesmo raciocínio vale para a parte superior, para acharmos a intensidade da força.
Logo:
O centroide do retângulo é encontrado na posição:
Essa posição em relação ao próprio diagrama, agora em relação a parede temos:
Passo 4
Com o que achamos, vamos calcular a força resultante:
Ele quer que , então
Passo 5
Agora vamos calcular a resultante do momento binário em relação a extremidade esquerda da viga, que vamos chamar de . Considerando o sentido anti-horário positivo