Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 6.Problemas - Ex. 7
Determine a força em cada membro da treliça e diga se os membros estão sob tração ou compressão. Faça .
Passo 1
Fala ai galerinha bonita, tudo beleza?!
Saca só, o problema quer que a gente encontre a força de cada membro mostrando se ele está sendo tracionado ou comprimido. Nesse caso, vamos analisar junta por junta (Método dos nós).
Então, vamos começar pelas forças da junta , porque tem apenas duas forças desconhecidas e possui uma que o problema deu.
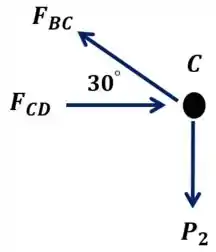
Sabendo que o somatório das forças no eixo e somatório das forças do eixo é , pois a estrutura encontra-se em equilíbrio.
No eixo primeiro:
Assim encontramos:
Estando tracionada.
Agora no eixo :
Então encontramos:
Nesse caso, estando sob compressão.
Passo 2
Agora, vamos analisar as forças da junta .
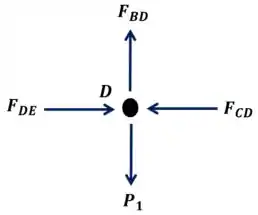
Sabendo que o somatório das forças no eixo e somatório das forças do eixo é , pois a estrutura encontra-se em equilíbrio.
No eixo primeiro:
Assim encontramos:
Estando em compressão.
Agora no eixo :
Então encontramos:
Nesse caso, estando sob tração.
Passo 3
Por fim, vamos fazer o mesmo na junta .
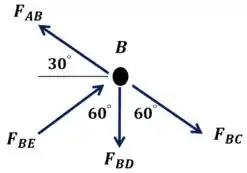
Lembrambro sempre que o somatório das forças no eixo e somatório das forças do eixo é , pois a estrutura encontra-se em equilíbrio.
No eixo primeiro:
Assim encontramos:
Estando sob tração.
Agora no eixo :
Então encontramos:
Estando também tracionada.
Resposta
(Tração)
(Compressão)
(Compressão)
(Tração)
(Compressão)
(Tração)