Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 148

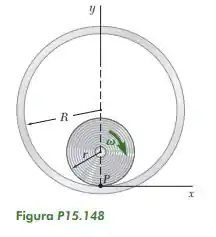
15.148. Uma roda de raio r rola sem escorregar ao longo do interior de um cilindro fixo de raio R com uma velocidade angular constante . Representando por P o ponto da roda em contato com o cilindro em t 0, deduza expressões para os componentes horizontal e vertical da velocidade de P em qualquer instante t. (A curva descrita pelo ponto P é uma hipocicloide.)

Passo 1

Vamos começar o problema definindo dois ângulos, θ e ϕ .

θ indica o movimento do ponto P em torno do círculo menor e ϕ indica a o movimento do circulo menor em torno do círculo maior.

Passo 2

A gente pode assumir que

d θ d t = ω

E

θ = ω t

A roda gira sem deslizar, então podemos concluir que o arco OC é igual ao arco PC.

Temos

P C = r θ + ϕ

E

O C = R ϕ

Sendo r o raio da roda interna e R o raio da roda externa.

Então

r θ + ϕ = R ϕ

Vamos isolar ϕ

R ϕ - r ϕ = r θ

ϕ R - r = r θ

ϕ = r θ R - r

Ou

ϕ = r ω t R - r

A derivada fica

ϕ ˙ = r ω R - r

Passo 3

Agora podemos assumir que

x = R - r sin ⁡ ϕ - r sin ⁡ θ

E

y = R - R - r cos ⁡ ϕ - r cos ⁡ θ

Vamos derivar

x ˙ = v x = R - r ϕ ˙ cos ⁡ ϕ - r θ ˙ cos ⁡ θ

Substituindo os valores de ϕ e ϕ ˙ temos

v x = R - r r ω R - r cos ⁡ r ω t R - r - r ω cos ⁡ ω t

Isso fica

v x = r ω cos ⁡ r ω t R - r - cos ⁡ ω t

E

y ˙ = v y = R - r ϕ ˙ sin ⁡ ϕ + r θ ˙ sin ⁡ θ

Substituindo os valores

v y = R - r r ω R - r sin ⁡ r ω t R - r + r ω sin ⁡ ω t

Isso fica

v y = r ω s in ⁡ r ω t R - r + sin ⁡ ω t

Resposta

v x = r ω cos ⁡ r ω t R - r - cos ⁡ ω t

v y = r ω sin ⁡ r ω t R - r + sin ⁡ ω t

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usando o método da Seção 15.14 , resolva o Problema 15.19 5 .
Uma placa quadrada com 500m m de lado está articulada nos pontos A e B de um grampo em U . A placa gira à taxa constante ω 2 = 4r a d / s em relação ao grampo, que, por sua vez, gira à taxa constante
O rotor de um motor elétrico tem a velocidade de 1.800 rpm quando a energia é desligada. O rotor é então observado até alcançar o repouso após executar 1.550 rpm. Considerando o movimento uniformement
Um ventilador de um motor de um automóvel gira em um eixo horizontal paralelo a direção de movimento do automóvel. Quando visto da retaguarda do motor, observa-se que o ventilador gira no sentido horá
Um ventilador de um motor de um automóvel gira em um eixo horizontal paralelo a direção de movimento do automóvel. Quando visto da retaguarda do motor, observa-se que o ventilador gira no sentido horá