Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 151

15.151. Duas barras rotativas estão conectadas por um bloco deslizante P. A barra presa em A gira com velocidade angular constante A. Para os dados fornecidos, determine para a posição mostrada nas figuras (a) a velocidade angular da barra presa em B, (b) a velocidade relativa do bloco deslizante P com relação à barra na qual ele desliza.

b = 3 00   m m ,   ω A = 10 r a d s  

Passo 1

Vamos matar mais uma! Nessa questão aqui começamos sabendo algumas coisas.

b = 3 00   m m ω A = 10 r a d s

E o exercício diz que a velocidade angular é constate, então

α A = 0

Com essas informações que temos a gente pode determinar as distancias A P - e B P - . Não vai ser muito complicado medir essas distancias, só precisamos usar a lei dos senos.

Vamos determinar ϕ . Olhando o triangulo vemos que

60 ° + ϕ = 180 °

Afinal, é uma linha reta. Então

ϕ = 180 ° - 60 ° = 120 °

Agora para determinar θ basta saber que a soma dos ângulos internos de um triângulo é igual a 180 ° . Então

20 ° + 120 ° + θ = 180 °

Logo

θ = 180 ° - 120 ° - 20 ° = 40 °

Agora ficamos com o triângulo

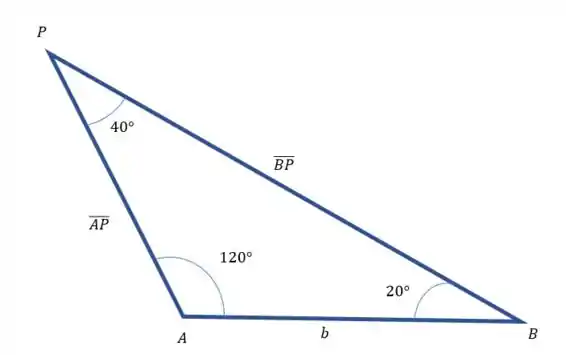
Usando a lei dos senos

b sin ⁡ 40 ° = A P - sin ⁡ 20 ° = B P - sin ⁡ 120 °

Então

A P - = b sin ⁡ 20 ° sin ⁡ 40 ° = 159,63   m m

B P - = b sin ⁡ 120 ° sin ⁡ 40 ° = 404,19   m m

Passo 2

Agora que juntamos informações suficientes do nosso sistema, vamos começar a calcular as velocidades. Vamos imaginar um ponto P’, que é o ponto onde o segmento A D - coincide com o bloco P . Nós podemos calcular a velocidade do ponto P’ assim:

v P ' = A P - ⋅ ω A

Então

v P ' = 159,63 ⋅ 10 = 1 596,3 m m s

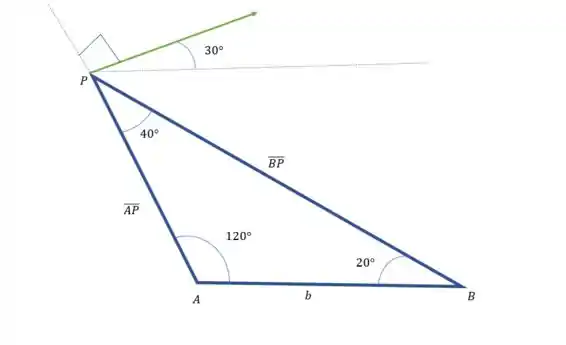
Podemos usar o teorema de Tales para descobrir o ângulo da velocidade.

Essa velocidade que acabamos de calcular é uma componente da velocidade no bloco P.

v P = v P ' + v B P

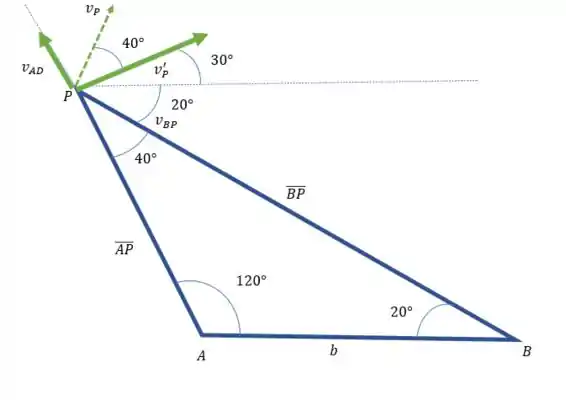
Passo 3

Olha só, a gente pode calcular v P da seguinte forma

v P = B P - ⋅ ω B

Mas a gente também pode calcular assim

v P ' = v P ⋅ cos ⁡ 40 °

v P = v P ' cos ⁡ 40 °

Então

B P - ⋅ ω B = v P ' cos ⁡ 40 °  

Agora a gente pode responder o item (a).

ω B = v P ' B P - ⋅ cos ⁡ 40 °

Substituindo os valores

ω B = 1596,3 404,19 ⋅ cos ⁡ 40 ° = 5,16 r a d s

Passo 4

Para responder o item (b) só precisamos determinar o valor de v A D , então

v A D = v P ⋅ sin ⁡ 40 °

Ou então

v A D = v P ' cos ⁡ 40 ° ⋅ sin ⁡ 40 °

Isso fica

v A D = v P ' ⋅ tan ⁡ 40 °  

Então

v A D = 1596,3 ⋅ tan ⁡ 40 ° = 1339,45 m m s = 1,339 m s

Com θ = - 20 ° em relação ao eixo x positivo.

Resposta

a :   ω B = 5,16 r a d s b : v A D = 1,339 m s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O movimento do bico D é controlado pelo braço AB. No instante mostrado, o braço está girando no sentido anti-horário a uma taxa constante w = 2,4 rad / s e a porção BC está sendo estendida a uma taxa
Resolva o Problema 15.221, supondo que no instante mostrado a velocidade angular ω 1 da haste é 3 rad / s e está aumentando a uma taxa de 12 rad / s², enquanto a velocidade relativa u do colar é 34 in
O guindaste mostrado gira a uma taxa constante col = 0,25 rad / s; simultaneamente, a lança telescópica está sendo abaixada a uma taxa constante ω 2 = 0.40 r a d / s . Sabendo que, no instante mostrad
Na posição mostrada, a haste fina se move a uma velocidade constante u = 3 in./s para fora do tubo BC. Ao mesmo tempo, o tubo BC gira a uma taxa constante ω 2 = 1.5 r a d / s em relação ao braço CD. S
Na posição mostrada, a haste fina se move a uma velocidade constante u = 3 pol./s para fora do tubo BC. Ao mesmo tempo, o tubo BC gira a uma taxa constante de ω 2 = 1.5r a d/ s em relação ao braço CD.