Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 92

Um membro em compressão de 3m de comprimento efetivo é feito, parafusando-se juntos dois perfis laminados de aço L102x76x6,4, como mostrado. Sabendo-se que σ e = 250   M P a   e   E = 200 G P a , determinar a carga centrada admissível para este membro comprimido.

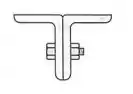
Passo 1

Vamos trazendo as informações partiu?

Aço: σ y = 250 × 10 6 P a     E = 200 × 10 9 P a

C c = 2 π 2 E σ y = 2 π 2 200 × 10 9 250 × 10 6 = 125,664

Passo 2

Agora a gente começa tentar diferentes perfis (que estão no apêndice) do livro para vermos o que se encaixa com nossa necessidade

T e n t e   L 89 × 64 × 9,5 .    

A = 20 1360 = 2720 m m 2 = 2720 × 10 - 6 m 2

I x = 2 1,07 × 10 6 = 2,14 × 10 6 m m 4

I y = 2 0,463 × 10 6 + 1360 16,9 2 = 1,70285 × 10 6 m 4 = I m i n

r = I m i n A = 1,70285 × 10 6 2720 = 25,021 m m = 25,021 × 10 - 3 m

L e r = 2,4 25,021 × 10 - 3 = 95,919 < C c L e r C c = 0,76330

Determinando o fator de segurança para esse perfil temos:

F . S . = 5 3 + 3 8 0,76330 - 1 8 0,76330 3 = 1,8973

σ μ = σ y F . S . 1 - 1 2 L e r C c 2 - 250 × 10 6 1,8973 1 - 1 2 0,76330 2 = 93,38 × 10 6 P a

P μ = σ μ A = 93,88 × 10 6 2720 × 10 - 6 = 254 × 10 3 N = 254 k N < 325 k N

Não use pois o valor encontrado é menor que o previsto, vamos a outro perfil

Passo 3

T e n t e   L 89 × 64 × 12,7      

A = 2 1780 = 3560 m m 2 = 3560 × 10 - 6 m 2

I x = 2 1,36 × 10 6 = 2,72 × 10 6 m m 4

I y = 2 0,581 × 10 6 + 1780 18,1 2 = 2,3283 × 10 6 m m 4 ∙ I m i n

r = I A = 2,3283 × 10 6 3560 = 25,574 m m = 25,574 × 10 - 3 m

L e r = 2,4 25,574 × 10 - 3 = 93,846 < C c                       L e r C c = 0,7468

Passo 4

Vamos determinar o fator de segurança :D

F . S . = 5 3 + 3 8 0,7468 - 1 8 0,7468 3 = 1,89465

σ μ = 250 × 10 6 1,89465 1 - 1 2 0,7468 2 = 95,155 × 10 6 P a

P μ = σ μ A = 95,155 × 10 6 3560 × 10 - 6 = 339 × 10 3 N = 339 k N > 325 k N

Como é maior não tem perigo e atende aos requisitos :D

U s e   L 89 × 64 × 12,7

Resposta

L 89 × 64 × 12,7

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um membro em compressão tem a seção transversal mostrada e um comprimento efetivo de 2m. Sabendo-se que a liga de alumínio usada é 2014-T6, determinar a carga centrada admissível.
Um membro em compressão de comprimento efetivo igual a 9 m é obtido soldando-se duas placas de aço de 10 mm de espessura a um perfil laminado de aço w250 x 80, como mostrado. Sabendo que σ= 320 MPa e
Resolver o problema 11.100 assumindo que o comprimento efetivo do membro comprimido é aumentado para 2,75 m.
Um membro em compressão de comprimento efetivo igual a 9 m é obtido soldando-se duas placas de aço de 10 mm de espessura a um perfil laminado de aço w250 x 80, como mostrado. Sabendo que σ= 320 MPa e
Um membro em compressão tem a seção transversal mostrada em um comprimento efetivo de 1,5m. Sabendo-se que a liga de alumínio usada é 6061 - t 6 , determinar a carga a carga centrada admissível.