Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 113
Usando a liga de alumínio 2014-T6, determinar o maior diâmetro admissível da barra de alumínio AB para uma carga centrada P de intensidade igual a: (a) 108 kN; (b) 166 kN
Passo 1
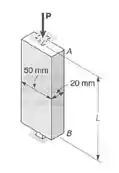
Galerinha, vamos ver os dados que temos para usarmos as fórmulas e realizar nosso cálculo:
Passo 2
(a)
Passo 3
(b)
Resposta
Resposta
Então gurizada, como acabamos de calcular, temos a resposta de
Exercícios de Livros Relacionados
Uma carga centrada P deve ser suportada pela barra de aço AB. Sabendo-se que σ e = 250M P aeE = 200G P a , determinar a menor dimensão d da seção transversal que pode ser usada, quando : (a) P = 60k N
Uma carga centrada de 200 kN é aplicada a uma coluna de madeira de 5,8m de comprimento efetivo. Usando um tipo de madeira para a qual E = 12G P a e a tensão admissível à compressão, paralela às fibras
Uma coluna de madeira AB está livre em seu topo A, engastada em sua base B e suporta uma carga de 52 kN, como indicado. Para o tipo de madeira usada E = 112G P a e a admissível à compressão, paralela
Um membro de aço comprimido, de 2,3m de comprimento efetivo, suporta uma carga excêntrica, como mostrado. Usando o método da tensão admissível, determinar a carga admissível P. Assumir E = 200 G P aeσ
Uma carga excêntrica é aplicada em um ponto, a 30mm do eixo geométrico, de uma barra de 56 mm de diâmetro, feita da liga de alumínio 6061-T6, para a qual a tensão admissível em flexão é 150 Mpa. Usand