Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.9 - Ex. 200
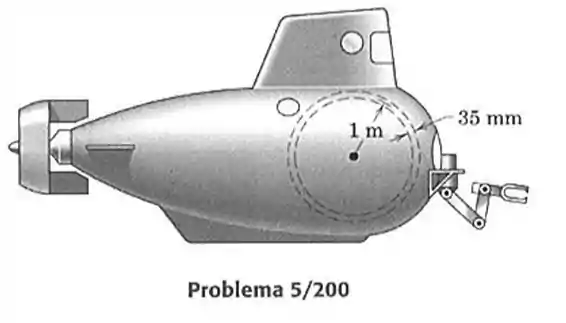
200- O submarino de pesquisa para grandes profundidades tem um compartimento de passageiros na forma de uma casca esférica, feita em aço, com um raio médio de e uma espessura de . Calcule a massa do lastro de chumbo que o submarino deve carregar de modo que o peso combinado da casca de aço e do lastro de chumbo cancele exatamente a flutuabilidade combinada apenas dessas suas partes. (Consulte a tabela , apeêncice , quando necessário.)
Passo 1
O sistema de forças desse submarino pode ser reduzido para o sistema de forças na casca de aço e do lastro de chumbo de forma que temos o seguinte sistema abaixo:
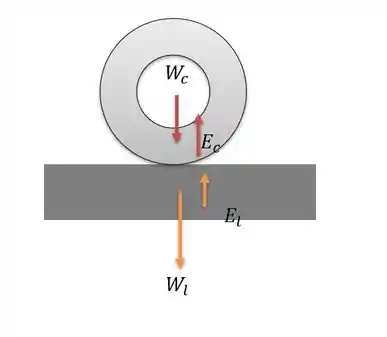
Onde é o empuxo da casca, é o empuxo do lastro, são os pesos, logo para haver o equilíbrio no sistema temos:
Antes de calcular as forças vamos pegar na tabela no anexo as densidades dos materiais:
Subtende-se que o submarino é utilizado em água salgada.
Passo 2
Vamos nos preocupar com a casca esférica, o volume total ocupada (isso é o volume de ocupação na água)por essa casca será o volume total da esfera, isso é o raio médio mais a metade da espessura, isso é importante para o cálculo do empuxo.
Agora para o peso somente o volume físico da casca gerará peso para a esfera. Isso é o volume total ocupada pela esfera diminuído pelo espaço em branco (que seria ocupada pelas esferas.
Logo o peso da esfera será:
Passo 3
Agora para o lastro de chumbo, temos o peso do lastro igual a:
E o empuxo:
Agora substituindo todos esses resultados no sistema de forças nós teremos: