Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.9 - Ex. 192

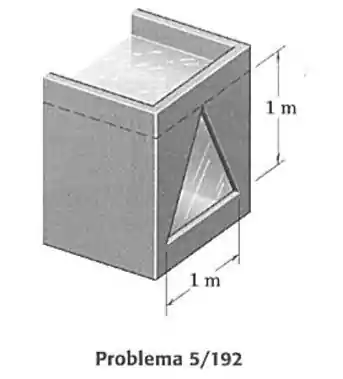
192- Determine a força total R exercida sobre a janela triangular pela água doce no tanque. O nível da água coincide com o topo da janela. Determine, também, a distância H , desde R até o nível da água.

Passo 1

Para calcular a força da água na janela nós precisamos saber a área dessa figura e a pressão média. Como o centroide é medido desde o nível da água até o ponto médio, nós temos que:

h - = 2 3 1 = 2 3

Logo:

R = ρ g h - A = 1000 × 9.81 × 2 3 × 1 × 1 2 = 3270   N

Passo 2

Já a distância H onde a força de R atua é a distância do centroide do tetraedro de força atuante no vidro da janela.

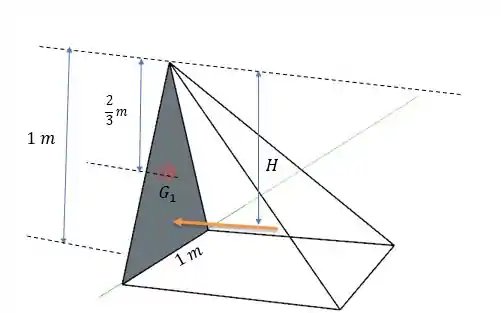
E o centro de um tetraedro medido do nível da água é dada por:

H = 3 4 l

Tal como pode ser visto na tabela D 4 , qualquer pirâmide tem altura z - medida da sua base igual a h / 4 .

H = 3 4 m

Resposta

R = 3270   N

H = 3 4 m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine os componentes x e y de cada uma das forças indicadas.
O cabo A C exerce sobre a viga A B a força P dirigida ao longo da linha A C . Sabendo que P tem uma componente vertical de 1560N , determine (a) a intensidade da força P , (b) sua componente horizonta
Determine os componentes x e y de cada uma das forças indicadas.
O cabo de sustentação B D exerce no poste telefônico A C uma força P dirigida ao longo de B D . Sabendo que P tem uma componente de 180N perpendicular ao poste A C , determine (a) a intensidade da for
Determine os componentes x e y de cada uma das forças indicadas.