Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.9 - Ex. 103

O jardineiro de 80 kg se abaixa com a corda sobre um galho horizontal da árvore. Se o coeficiente de atrito entre a corda e o galho vale 0,60, calcule a força que o homem deve fazer na corda para se abaixar lentamente.

Passo 1

Devemos considerar que o homem e a corda se movimentam a velocidade constante, então valem para eles as equações de equilíbrio. A fórmula para o equilíbrio da corda é a seguinte:

ln ⁡ T 2 T 1 = μ β

Sendo T 2 e T 1 as trações maior e menor nas extremidades da corda, μ o coeficiente de atrito entre a corda e o galho e β o ângulo total de contato da corda com a superfície, nesse caso igual a π , o ângulo de meia volta. O que queremos é encontrar a tração menor T 1 , feita na parte da corda que o homem está segurando, e pra isso precisamos da relação entre essa tração e a tração maior T 2 feita na parte que está amarrada no homem.

Passo 2

Vamos encontrar a relação entre T 1 e T 2 isolando o homem em um diagrama de corpo livre:

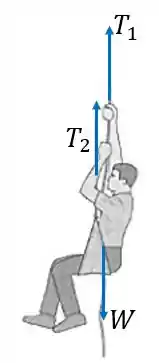
Através da equação do equilíbrio vertical, encontramos a relação entre T 1 e T 2 . O enunciado diz que a massa do homem é de 80 kg.

∑ F = 0 ⇒ T 1 + T 2 = m g

⇒ T 1 + T 2 = 80 × 9,81 = 784,8

Então temos T 2 em função de T 1 :

T 2 = 784,8 - T 1

Passo 3

Agora podemos aplicar a fórmula para achar T 1 :

ln ⁡ T 2 T 1 = μ β

⇒ ln ⁡ 784,8 - T 1 T 1 = 0,6 × π

Colocando na forma exponencial e isolando T 1 :

784,8 - T 1 T 1 = e 0,6 π ⇒ 784,8 - T 1 = T 1 e 0,6 π

⇒ 784,8 = T 1 ( 1 + e 0,6 π )

⇒ T 1 = 784,8 1 + e 0,6 π = 103,5   N

Resposta

T 1 = 103,5   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A biela está conectada ao pistão por um pino com diâmetro de 20m m em B e ao virabrequim por um mancal A com diâmetro de 50m m . Se o pistão estiver se movendo para baixo e o coeficiente de atrito est
A polia é suportada por um pino de 25m m de diâmetro. Se a polia se ajusta livremente no pino, determine a maior força P que pode ser aplicada à corda e ainda baixar o balde. O balde tem uma massa de
A viga de aço de 1,2 toneladas é movida sobre uma superfície nivelada usando uma série de roletes com diâmetro de 30m m , para os quais o coeficiente de resistência a rolamento é 0,4m m no solo e 0,2m
O carrinho, juntamente com a carga, pesa 750N( ≈ 75k g ) . Se o coeficiente de resistência ao rolamento é a = 0,75m m , determine a força necessária para puxar o carrinho com velocidade constante.
O rolo compressor tem uma massa de 80k g . Se o braço B A for mantido a um ângulo de 30 ° da horizontal e o coeficiente de resistência ao rolamento para o cilindro for 25m m , determine a força P nces