Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 3.Problemas - Ex. 20

2.21. Se Φ = 30 ° e a força resultante deve ser de 6   k N , orientada ao longo do eixo y positivo, determine as intensidades de F 1   e   F 2 e o ângulo θ, se F 2 necessita ser mínima.

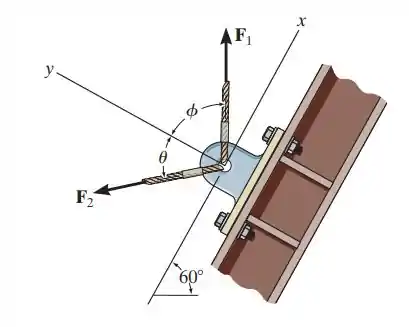
Passo 1

Para F 2 ser mínima ela deve ser perpendicular a F 1 .

Vamos analisar os vetores F 1 , F 2 e F R   como vetores, e aí poderemos usar a lei dos paralelogramos, vou desenhar isso.

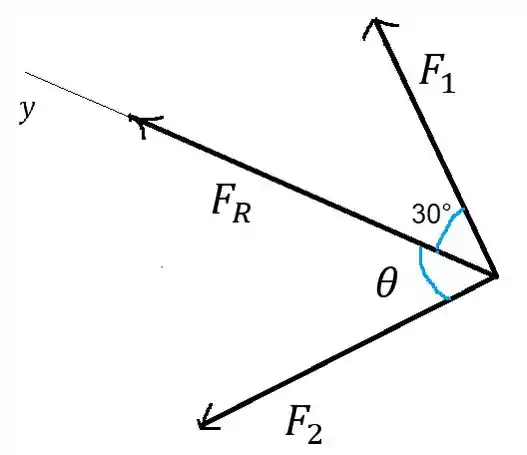
Passo 2

Agora podemos determinar F 1   e   F 2 , usando trigonometria

F 1 = F R ⋅ cos ⁡ 30 ° = 6 ⋅ cos ⁡ 30 ° = 5,20   k N F 2 = F R ⋅ sin ⁡ 30 ° = 6 ⋅ sin ⁡ 30 ° = 3   k N

Passo 3

Agora para determinar o ângulo θ basta lembrar que o ângulo entre F 1   e   F 2 é 90°, então

90 ° = θ + 30 ° θ = 90 ° - 30 ° = 60 °

Resposta

F 1 = 5,20   k N F 2 = 3   k N θ = 55,1 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine  a  intensidade  da  força  resultante  que atua sobre a chapa de fixação de uma treliça de  ponte.
Se a intensidade da força resultante que atua sobre o suporte for 80N direcionada ao longo do eixo u , determine a intensidade de F e sua direção θ .
Determine a intensidade da força resultante que atua sobre a cantoneira e sua direção θ , medida no sentido anti-horário a partir do eixo x .
Decomponha F em componentes ao longo dos eixos u e v e determine as intensidades dessas componentes.