Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 32
32. Um tubo de papel é formado enrolando-se uma tira de papel em espiral e colando as bordas como mostra a figura. Determine a tensão de cisalhamento que age ao longo da linha de junção localizada a em relação á vertical, quando o tubo é submetido a uma força axial de . O papel tem de espessura e o tubo tem diâmetro externo de .
Passo 1
Fala galerinha bonita, tudo jóia?
Saca só, nesse exercício aqui o enunciado nos diz que um tubo de papel é formado enrolando-se uma tira de papel em espiral e colando as bordas como na figura mostrada, então sabendo disso o enunciado quer que a gente determine a tensão de cisalhamento que age ao longo da linha de junção quando o tubo é submetido a uma força axial de !
Belezoca, se a gente analisar bem essa figura, vamos reparar ali uma força de , que faz um ângulo de com a seção transversal do tubo. Logo, o único tipo de tensão presente no nosso sisteminha ali, é a tensão normal, que conveniente vamos chamar de .
A questão nos diz também, o valor do ângulo das linhas de junção com a vertical, igual a , que é o ângulo que utilizaremos em nossos cálculos.
Maravilha, então bora lá ver como que fica essa brincadeira!
Passo 2
A única tensão presente no nosso sistema, é aquela originada da força axial de , que é uma tensão normal. E qual é mesmo a fórmula da tensão normal?
Isso mesmo! A fórmula da tensão normal é dada pela divisão da força perpendicular à fibra pela área da seção transversal. Mas temos que tomar atenção no cálculo da área, pois a própria questão diz o tubo tem uma certa expessura. Logo terá um diâmetro interno e um externo. Nossa fórmula então, vai ficar assim:
E chegamos ao seguinte estado plano de tensão:
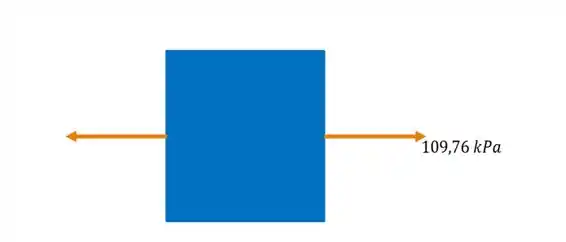
Onde:
Passo 3
Agora, só resta a gente aplicar a fórmulas da transformação de tensão para o caso cisalhante, que tem a seguinte cara:
Substitui-se os valores numéricos pertinentes a cada variável, dado o valor do ângulo .
E encontramos nossos resultado igual à: