Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 24
24. As fibras da madeira da tábua formam um ângulo de com a horizontal como mostra a figura. Determine a tensão normal e a tensão de cisalhamento que agem perpendicularmente às fibras, se a tábua é submetida a uma carga axial de .
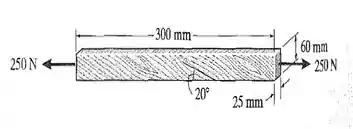
Passo 1
E aí galerinha bonita, tudo bem? Aqui vamos nós de novo pra mais uma questãozinnha de ResMat.
Existem duas formas pra gente calcular as tensões perpendiculares às fibras, a mais tranquileba seria decompor a força P em Normal e Tangencial e calcular as tensões sobre uma área inclinada. Porém este capítulo tem exercícios referentes ao estado planos de tensões, então a gente vai ter que fazer nesse estilo, ok?
Vamos representar as tensões e do plano inclinado:
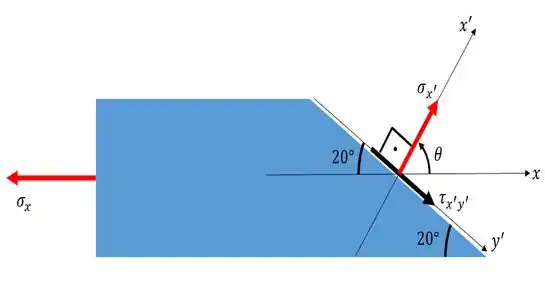
A força de vai gerar uma tensão no eixo , que chamamos de , e essa tensão é perpendicular à seção transversal retangular da tábua.
Passo 2
Para que a gente possa relacionar as tensões no plano, com as tensões no plano inclinado, podemos usar as fórmulas abaixo:
Pela figura do , podemos ver que é positivo (rotação em sentido anti-horário) e o seu valor vai ser igual ao complementar de . Ou seja...
Agora, vamos à obtenção das tensões de estado plano!
Passo 3
A única tensão presente no nosso sistema, é aquela originada da força axial de , que é uma tensão normal agindo no eixo . E já sabemos que ela é dada pela fórmula abaixo, né?
Substituindo os valores numéricos, obtemos que...
E então chegamos até a figura a seguir, que retrata o estado plano de tensão:
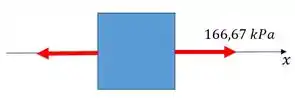
Onde:
Passo 4
E pra terminar, só resta a gente aplicar as fórmulas de transformações de tensão para os casos normal e cisalhantes. São elas:
Onde substituindo os valores numéricos pertinentes a cada variável, dado o valor do ângulo ...
Encontramos nossos resultados, iguais à:
E tá prontinho!