Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 127

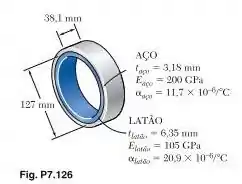
Um anel de latão com diâmetro externo de 127   m m e espessura de 6,35   m m   se encaixa exatamente dentro de um anel de aço com diâmetro interno de 127   m m   e 318   m m   de espessura, quando a temperatura de ambos é de 10 ° C .   Sabendo que a temperatura dos dois anéis e então aumentada para 51,7 ° C ,   determine (a) a tensão de tração no anel de aço e (b) a pressão correspondente aplicada pelo anel de latão no anel de aço.

Passo 1

Fala aí, galerinha. Tudo bem com vocês? Vamos para outra questão.

Sabemos que, a pressão interna no anel de aço causa uma tensão que é dada por:

σ a ç o = p r t a ç o

Onde t   é a espessura do anel de aço, r   o raio e p   a pressão.

A deformação correspondente a esta pressão é dada pela lei de Hook:

ε a ç o 1 = σ a ç o E a ç o = p r E a ç o t a ç o

No entando, também há uma deformação causada pela temperatura, que será:

ε a ç o 2   = α a ç o ∆ T

Portanto, a deformação total será:

ε t o t a l = ε a ç o 1 + ε a ç o 2 = p r E a ç o t a ç o + α a ç o ∆ T

Logo, a mudança no comprimento do anel será:

∆ L a ç o = 2 π r ε t o t a l = 2 π r p r E a ç o t a ç o + α a ç o ∆ T

Passo 2

Agora, faremos a mesma coisa para o anel de latão. Sabemos que:

σ l a t ã o = p r t l a t ã o

Logo, a deformação correspondente seá:

ε l a t ã o 1 = p r E l a t ã o t l a t ã o

E a deformação por temperatura será:

ε l a t ã o 2   = α l a t ã o ∆ T

Logo, a mudança na circunferência será:

∆ L l a t ã o = 2 π r ε l a t ã o = 2 π r p r E l a t ã o t l a t ã o + α l a t ã o ∆ T

Passo 3

Como os anéis estão unidos, eles terão a mesma deformação circunferencial. Portanto:

∆ L a ç o = ∆ L l a t ã o

2 π r p r E a ç o t a ç o + α a ç o ∆ T = 2 π r p r E l a t ã o t l a t ã o + α l a t ã o ∆ T

Logo, simplificando e arrumando:

r E a ç o t a ç o + r E l a t ã o t l a t ã o p = ( α l a t ã o - α a ç o ) ∆ T

Onde a nossa única incógnita será a pressão p .   Substituindo os valores, teremos:

∆ T = 51,7 - 10 = 41,7 ° C

Logo, isolando p   e substituindo os dados fornecidos:

p = 1 , 57   M P a

Essa é a letra b.

Passo 4

Para a letra a, basta substituir na fórmula da tensão:

σ a ç o = p r t a ç o

Logo:

σ a ç o = 15,71   M P a

Resposta

  1. σ a ç o = 15,71   M P a
  2. p = 1 , 57   M P a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o estado de tensões dado, determine (a) os planos principais e (b) as tensões principais.
Para o estado de tensões dado, determine as tensões normal e de cisalhamento depois que o elemento mostrado sofreu uma rotação de (a) 25 ° no sentido horário e (b) 10 ° no sentido anti-horário.
Para os estados de tensão mostrados nas figuras, determine as tensões normal e de cisalhamento que atuam na face oblíqua do elemento triangular sombreado na figura. Use um método de análise com base n
Para o estado de tensões dado, determine (a) a orientação dos planos de máxima tensão de cisalhamento no plano de tensões e (b) a tensão normal correspondente.
Para o estado de tensões dado, determine (a) a orientação dos planos de máxima tensão de cisalhamento no plano de tensões e (b) a tensão normal correspondente.