Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 21
21. A tensão que age nos dois planos em um ponto é indicada na figura. Determine a tensão normal e as tensões principais no ponto.
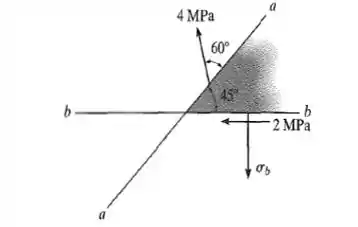
Passo 1
Bem! Vamos analisar a figura do enunciado. A questão pede basicamente, a tensão normal no plano e as principais. Agora se você analisar bem esse plano, vai reparar ali uma tensão . Pois bem, essa é a tensão normal em . E se for parar pra pensar um pouco, conclui-se que o , nada mais é do que a transformação de tensão nesse plano. Mas transformação de tensão de que?
Aí que está! Nossa é resultado da transformação de tensão lá daquela outra presente na figura do enunciado no plano , de . Ora bolas, o que temos que fazer, então é achar as tensões no plano e usar aquelas famigeradas equações de transformações para tensão, que já conhecemos. Vamos lá!
Passo 2
A única tensão presente no plano é aquela de . Mas se você reparar bem, ela pode ser decomposta em outras duas tensões, sendo que uma vai ser perpendicular ao plano e a outra vai ser paralela ao plano, nele contido. Ora, vamos ter então, uma tensão normal e uma tensão cisalhante . Bora calculá-las:
é dada por:
E é dada por:
Passo 3
Agora, analisemos o plano . Desse plano, tiramos que:
Eureca! Se temos o valor de ,, e do ângulo entre os plano e , que é , vamos usar então a equação de transformação para , para ver se arrumamos alguma coisa:
Substitui-se os valores numéricos pertinentes a cada variável:
Ia lá! Não é que obtivemos o valor de ?! Acho que com isso, já podemos achar a tensão normal no plano , né? Vamos ver:
Substitui-se o valor de cada variável na fórmula e chega-se então, à:
Passo 4
Agora, só falta descobrir as tensões principais, que são dadas através da seguinte fórmula:
Substituímos os valores numéricos adequados:
Mas não vamos esquecer que essa fórmula nos dá uma tensão máxima e uma tensão mínima . Para encontrar as duas, tá na cara que ná máxima basta somar e na mínima basta subtrair. Logo: