Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 34

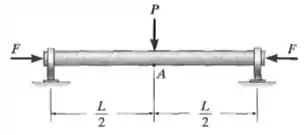
34. O eixo tem diâmetro d e está sujeito às cargas mostradas. Determine as tensões principais e a tensão de cisalhamento máxima no plano desenvolvidas no ponto A. Os mancais suportam apenas reações verticais.

Passo 1

Aqui, vamos primeira montar os diagramas de corpo livre da viga:

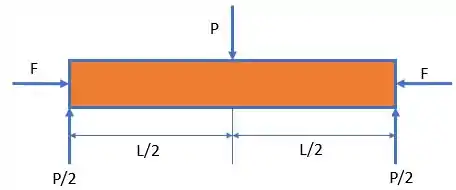
Como a força está no centro da barra e ela é homogênea, as reações serão iguais nos dois apoios.

Agora, faremos o diagrama de esforço cortante e momento fletor:

Com isso, é só realizar a análise dos esforços cortantes e momento fletor:

↶ + ∑ M = 0

M - 0,5 P 0,5 L = 0  

M = 0,25 P L

→ + ∑ F x = 0

N - F = 0  

N = F

↑ + ∑ F y = 0

0,5 P - V = 0  

V = 0,5 P

Passo 2

Como calculamos os resultados comuns aos dois pontos, iremos dividir a questão, resolvendo primeiro que foi pedido para o ponto A e depois para o ponto B .

Agora, vamos realizar o cálculo da tensão no ponto A , lembrando que a fórmula do momento polar de inércia de um círculo é da por π c 4 / 4 , onde c é a distância do centro até a borda mais externa:

σ A = - N A - M y A I

σ A = - F π 4 d 2 - P L 4 c π 4 c 4

σ A = 8 P L π d 3 - 4 F π d 2 = 4 π d 2 2 P L d - F   ( U n i d a d e s   e m   P a s c a l )

E agora, bora pro cálculo da tensão máxima de cisalhamento no ponto A :

τ A = V Q A I t

Como Q A = 0 :

τ A = 0   ( U n i d a d e s   e m   P a s c a l )      

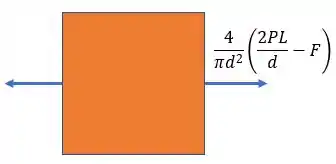
Passo 3

Calcularemos, então, as tensões principais no ponto A :

σ 1,2 = σ x + σ y 2 ± σ x - σ y 2 2 + τ x y 2

σ 1,2 = 8 P L π d 3 - 4 F π d 2 + 0 2 ± 8 P L π d 3 - 4 F π d 2 + 0 2 2 + ( 0 ) 2

σ 1,2 = 2 π d 2 2 P L d - F ± 2 π d 2 2 P L d - F

Vamos então, obter duas tensões; uma máxima σ 1 e uma mínima σ 2 :

σ 1 = σ x = 4 π d 2 2 P L d - F   ( U n i d a d e s   e m   P a s c a l )

σ 2 = σ y = 0   ( U n i d a d e s   e m   P a s c a l )

Passo 4

Por último, vamos calcular a tensão de cisalhamento máxima no plano τ m á x :

τ m á x = σ x - σ y 2 2 + τ x y 2

τ m á x = 8 P L π d 3 - 4 F π d 2 - ( 0 ) 2 2 + ( 0 ) 2

τ m á x = 2 π d 2 2 P L d - F 2 + ( 0 ) 2

τ m á x = 2 π d 2 2 P L d - F   ( U n i d a d e s   e m   P a s c a l )

Resposta

Tensões principais no ponto A :

σ 1 = σ x = 4 π d 2 2 P L d - F   ( U n i d a d e s   e m   P a s c a l )

σ 2 = σ y = 0   ( U n i d a d e s   e m   P a s c a l )

Tensão de cisalhamento máxima no ponto A :

τ m á x = 2 π d 2 2 P L d - F   ( U n i d a d e s   e m   P a s c a l )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

14. O estado de tensão em um ponto é mostrado no elemento. Determine:(a) as tensões principais e (b) a tensão de cisalhamento máxima no plano e a tensão normal média no ponto. Especifique a orientação
15. O estado de tensão em um ponto é mostrado no elemento. Determine:(a) as tensões principais e (b) a tensão de cisalhamento máxima no plano e a tensão normal média no ponto. Especifique a orientação
Sabendo que σ a d m = 165M P a e τ a d m = 100M P a selecione o perfil de mesa larga mais econômico que deverá ser utilizado para suportar o carregamento mostrado. () Determine os valores a serem espe
43. A viga tem seção transversal retangular e está sujeita às cargas mostradas. Determine as tensões principais desenvolvidas no ponto A e no ponto B , localizado imediatamente à esquerda da carga de
26. A viga T está sujeita ao carregamento distribuído aplicado ao longo de sua linha central. Determine as tensões principais nos pontos A e B e mostre os resultados em elementos localizados em cada u