Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 34
34. Para a viga e o carregamento mostrados nas figuras, (a) trace os diagramas de esforço cortante e de momento fletor, (b) determine os valores absolutos máximos do esforço cortante e do momento fletor.
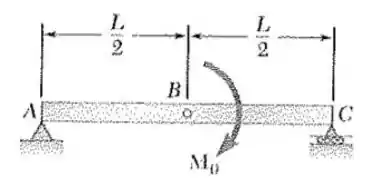
Passo 1
Bom! Vamos dar uma olhadinha na figura do enunciado e ver onde podemos começar nossa análise:
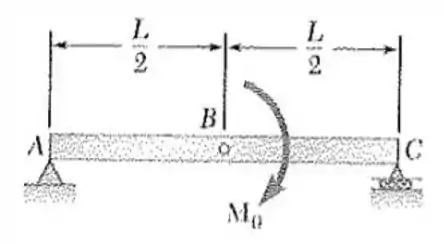
Olha só! A primeira coisa que temos que fazer é definir por onde vamos começar nosso estudo. Que tal fazermos isso, com nossa direção indo do ponto até o ponto ?
Sendo assim, se começarmos pelo ponto , vamos ter que descobrir as reações em e . Para isso, façamos o diagrama de corpo livre:
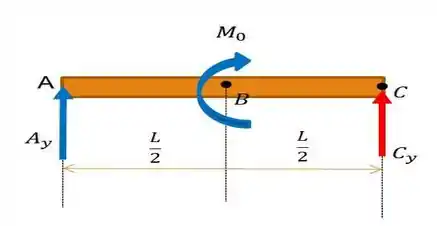
E para obter o valor das reações, primeiro façamos o somatório dos momentos em relação a um ponto de interesse, o ponto , que tal?
Depois, para obter , bora fazer o somatório das forças no eixo :
Passo 2
Agora, para descobrir os esforços cortantes e momentos fletores; temos que separar a viga em vários trechos e analisá-los separadamente, com nosso estudo indo do ponto até o :
Bora lá!! O primeiro trecho é o , e o diagrama de corpo livre para esse trecho está logo abaixo:
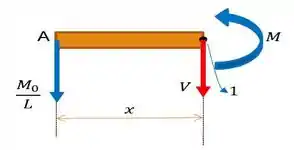
Diante dessa belezinha de imagem, fica até fácil saber o que temos fazer. Ora bolas! Para achar o esforço cortante, basta fazer o somatório das forças em . Olho lá, na nossa convenção adotada do esforço cortante, para baixo:
E para achar o momento fletor, tá vendo aquele ponto que nomeamos de na nossa figura. Pois bem! Vamos fazer o somatório dos momentos em relação a ele:
Pronto! Finalizamos o trecho , que vai de até :
Passo 3
Agora, bora partir pro trecho , com a nossa análise agora, indo de até . Para isso, bora lá fazer o esboço do nosso problema:
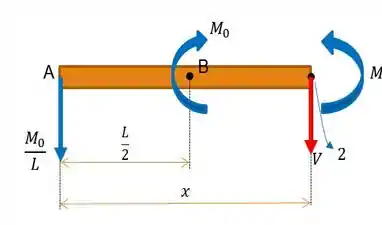
E como ninguém aqui é papagaio, bastar realizar os mesmos procedimentos do . Primeiro, o somatório das forças em :
Depois, o somatório dos momentos em relação ao ponto que nomeamos de . Olho lá nas distâncias entre as forças, hein!?
Pronto! Obtemos também as expressões para o trecho .
Passo 4
a) Com as seguintes expressões de esforço cortante e momento fletor, bora pro que interessa. Vamos calcular alguns pontos de interesse para construir o nosso gráfico:
Trecho :
Trecho :
E obtido esses valores, tracemos nosso gráfico:
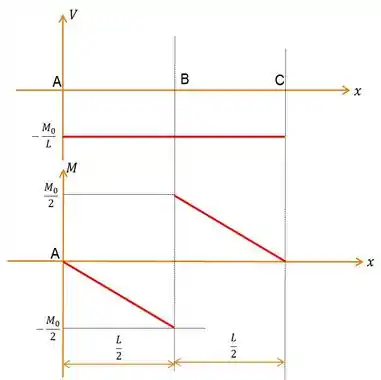
Passo 5
b) Finalmente, como a questão nos pede para determinar os valores absolutos máximos do esforço cortante e do momento fletor, o que temos que fazer nesse caso, é simplesmente usar a visão e ver qual o maior valor em módulo podemos extrair dos gráficos.
Trata-se portanto, de uma coisa simples e ao observar as figuras do , notamos que nossas respostas são dadas por:
Resposta
a)
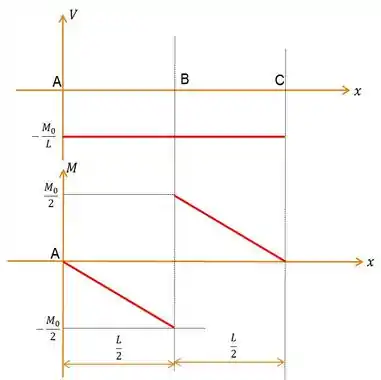
b)