Usando a propriedade indicada no Problema , determine a curva assumida por um cabo de vão e flecha que sustenta uma carga distribuida , onde é medido a partir do ponto médio do vão. Determine também os valores máximos e mínimo da tração do cabo.
Passo 1
Bom galera, vamos fazer um diagraminha de corpo livre, só pra facilitar nossa vida:
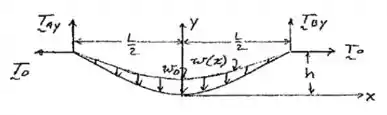
Onde o peso é dado por:
Passo 2
Show de bola, aplicando a propriedade do Problema , a gente fica com:
Logo, usando , nós temos:
Integrando mais uma vez, usando .
Passo 3
Então, vamos aplicar o que encontramos em um ponto que sabemos:
Agora ao isolarmos o , a gente fica com:
Que também á a tensão mínima.
Passo 4
Por fim, a gente precisa encontra a tensão máxima no cabo, e já sabemos que é a mínima, então a máxima tensão é , logo:
Isolando , ficamos com:
Logo:
Que é igual a tensão máxima: