Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 10.Problemas - Ex. 63
Usando o método da seção 10.8, resolva o probelma 10.35.
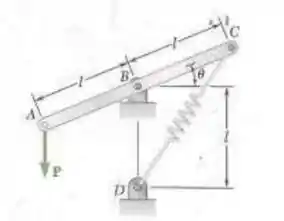
Passo 1
Fala aí galera, vamos para mais um problema de estática.
Sabemos que para encontrar a posição de equilíbrio, devemos encontrar a expressão da energia potencial e igualar sua derivada a 0. Logo, sabemos que:
Aplicando lei dos cossenos para determinar o tamanho da mola esticada:
Sabemos que a deformação da mola é dada por:
Portanto:
Vamos agora derivar a expressão:
Portanto, a expressão que satisfaz o equilíbrio será:
Passo 2
Agora, basta substituir os valores dados:
Resposta
Exercícios de Livros Relacionados
O caminhão tem uma massa de 200 Mg e um centro de massa G. Determine o grau de inclinação ao longo do qual ele possa estacionar sem tombar e investigue a estabilidade nessa posição.
A barra uniforme OA tem um peso de 100 N e quando ela está na posição vertical, a mola está livre. Determine a posição θ para o equilíbrio. Investigue a estabilidade na posição de equilíbrio.
A barra uniforme tem um peso W . Determine o ângulo θ para o equilíbrio. A mola está livre quando θ = 90 ° . Despreze o peso dos roletes.
Resolva o problema 11.56 usando o princípio de energia potencial. Investigue a estabilidade da barra quando ela está na posição de equilíbrio.
Determine a altura h do bloco B de modo que a barra esteja sempre em equilíbrio. As molas estão livres quando a barra está na posição vertical. O bloco tem um peso W .