Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 40
40- Considere a rede de voleibol mostrada na figura. Determine o ângulo formado pelos cabos de sustentação e .
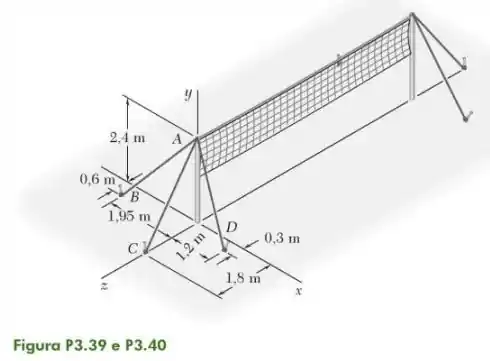
Passo 1
Agora queremos o ângulo formado entre e nessa rede que parece de vôlei de praia.
O vetor continua o mesmo da questão passada e que será:
Porém vamos fazer o módulo e a vetorização de
E o módulo será:
Passo 2
Logo pela definição de produto vetor será:
Substituindo:
Em graus o ângulo será:
Resposta
Exercícios de Livros Relacionados
Um carrinho de mão que se movimenta ao longo da viga horizontal é acionado por duas forças indicadas na figura. (a) Sabendo-se que α = 25 ° , determine, usando trigonometria, a intensidade da força P
Resolva o problema 2.3 usando trigonometria.
Dois elementos estruturais A e B são parafusados a um suporte, como mostra a figura. Sabendo que ambos os elementos estão em compressão e que a força é 15k N no elemento A e 10k N no elementro B . Det
Para o suporte tipo gancho do Problema 2.1, usando trigonometria e sabendo que a intensidade de P é 75N , determine (a) a intensidade requerida da força Q se a resultante R das duas forças aplicadas e
Dois elementos estruturais A e B são parafusados a um suporte, como mostra a figura. Sabendo que ambos os elementos estão em compressão e que a força é 1 0k N no elemento A e 1 5k N no elementro B . D