Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 34
34- Determine o valor de que minimiza a distância perpendicular de um ponto até a seção da tubulação que passa pelos pontos e .
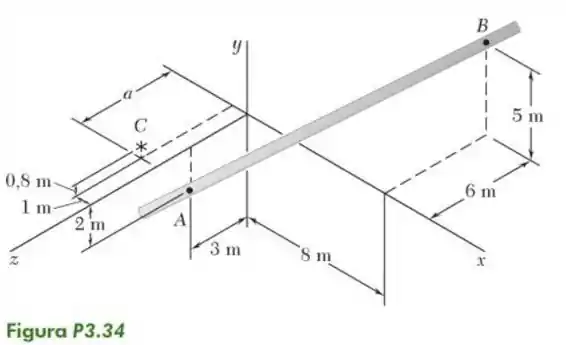
Passo 1
Para resolver este problema de forma física vamos considerar um momento em causado por uma força que encontra-se na seção que vai de até o momento em vale:
Vamos considerar uma força que vai de até e uma distância que vai de até , começando pela força nós teremos:
Isso nos dá:
E o vetor distância será:
Passo 2
Dessa forma o determinante do momento será:
Resolvendo esse determinante nós encontramos:
Isso nos dá um módulo igual a:
Passo 3
Desta forma a distância será:
Note que temos uma função em função de e para encontrarmos o menor valor de basta derivar uma vez em relação a e igualar a zero, isso nos fará encontrar um valor de necessário para que a pare de crescer ou decrescer e fique no ponto de mínimo local da função. Fazendo isso nós temos:
Isso nos dará: