Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 37
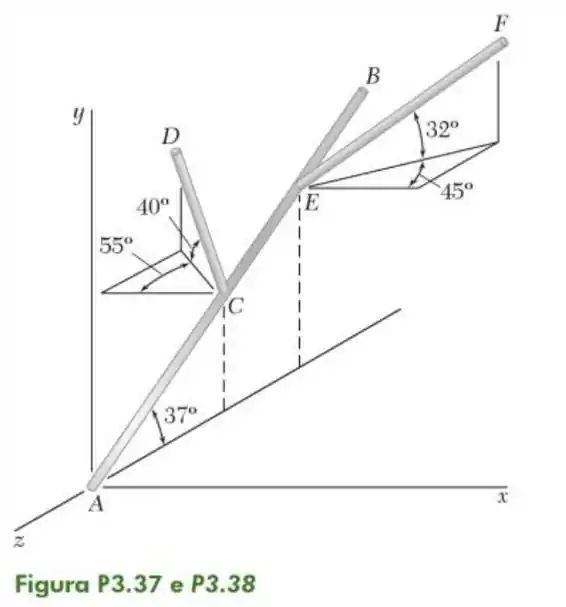
37- A seção de uma tubulação está no plano e forma um ângulo de com o eixo . Os ramais e são ligados como mostrado na figura. Determine o ângulo das linhas e .
Passo 1
Basicamente a questão pede o ângulo formando entre as linhas e e para isso usaremos a definição:
Onde os vetores e espelhados nos eixos coordenados serão iguais a:
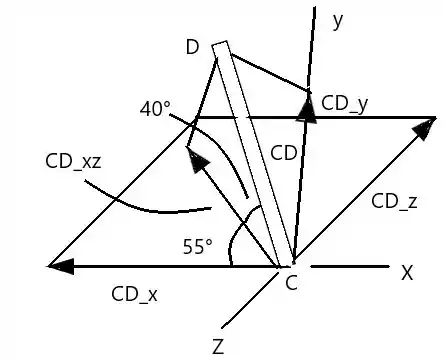
Note que a projeção em e em começando por estará indo contra a direção dos eixos ordenados. Além de termos que rebater o vetor no plano se quisermos saber os ângulos que essas linhas auxiliares fazem com eixos e .
Segue o diagrama
Passo 2
Logo aplicando a definição de multiplicação vetorial temos:
Fazendo essa conta em graus nós teremos:
Resposta
Exercícios de Livros Relacionados
46. Dados os vetores P → = 4 i ^ - 2 j ^ + 3 k ^ , Q → = 2 i ^ + 4 j ^ - 5 k ^ e S → = S x i ^ - j ^ + 2 k ^ , determine o valor de S x para o qual os três vetores são coplanares.
41- Sabendo que a tensão no cabo A C é 1260N , determine a ) o ângulo entre o cabo A C e a barra A B , b ) a projeção em A B da força exercida pelo cabo A C no ponto A .
35- Dados os vetores P = 3 i - j + 2 k , Q = 4 i + 5 j - 3 k e S = - 2 i + 3 j - k , calcule os produtos escalares P . Q , P . S e Q . S .
40- Considere a rede de voleibol mostrada na figura. Determine o ângulo formado pelos cabos de sustentação A C e A D .
39- Considere a rede de voleibol mostrada na figura. Determine o ângulo formado pelos cabos de sustentação A B e A C .