No , determinar:
- a variação dos valores de para que
- o valor de para que a máxima tensão seja a menor possível e o correspondente valor de .
Passo 1
O nosso objetivo é determinar o valor de k na nossa equação, para isso precisamos lembrar de duas coisas:
Uma é que a nossa fórmula de tensão é dada pela seguinte equação
E a outra é que a fórmula que relaciona as duas situações é dada por:
Em que é a tensão na situação final e é a tensão inicial, considerando o mesmo momento agindo em ambas as situações. Para isso, o mais difícil no nosso problema é determinar o valor do momento de inércia na situação inicial e final, sendo assim teremos que:
Passo 2
Cálculo do momento de inércia na situação inicial:
-
Para ele precisamos fazer a seguinte relação.
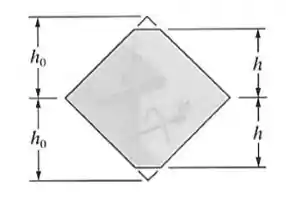
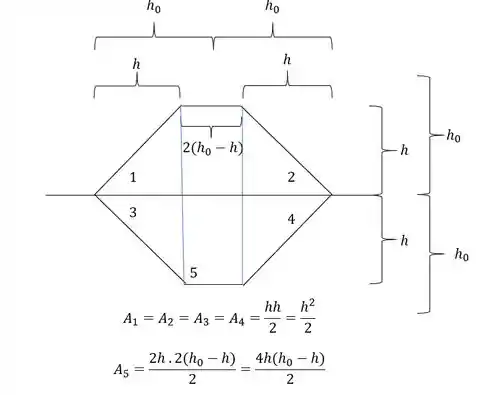
- Numeração das regiões
- Área das regiões
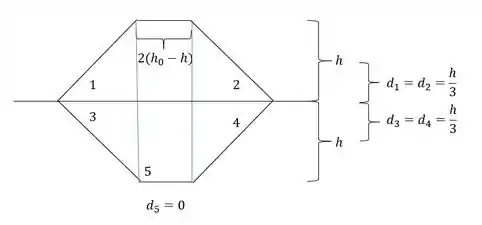
- Distância do centroide das áreas até a LN – aqui que vamos precisar da nossa LN
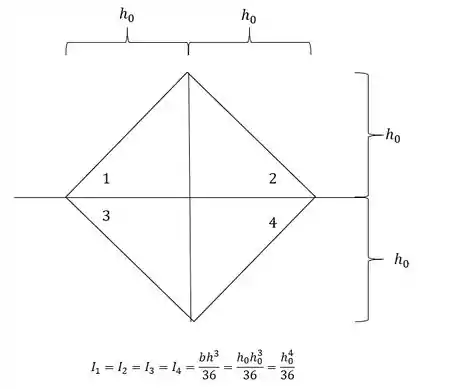
- Momento de inércia de cada região
Olha como esse macetinhos nos ajuda bastante.
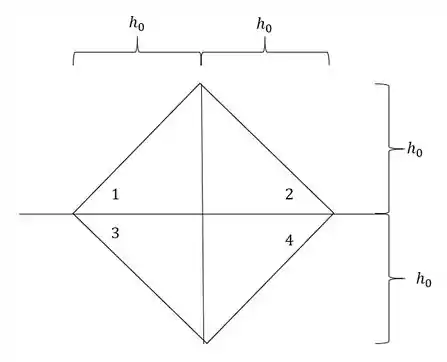
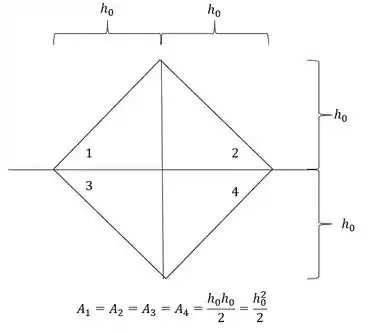
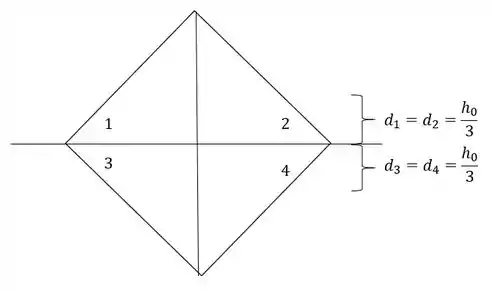
- positivo e negativo
-
Para ele precisamos fazer a seguinte relação.
- Numeração das regiões
- Área das regiões
- Distância do centroide das áreas até a LN – aqui que vamos precisar da nossa LN
- Momento de inércia de cada região
Olha como esse macetinhos nos ajuda bastante.
As medidas temos que:
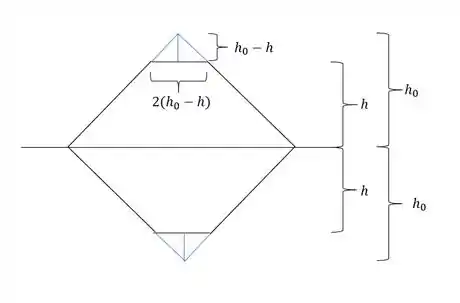

- positivo e negativo
Agora para determinarmos o momento de inércia, precisamos fazer a seguinte conta:
Mas temos que lembrar que precisamos usar os valores de inercia da região 6 como negativa, sendo assim temos que:
Agora só precisamos determinar os valores de y, sendo assim teremos que ver o próximo passo.
Passo 3
Determinando o valor de y, temos que:

Calculando a tensão teremos que:
Passo 4
Cálculo do momento de inércia na situação final:

Agora para determinarmos o momento de inércia, precisamos fazer a seguinte conta:
Mas temos que lembrar que precisamos usar os valores de inercia da região 6 como negativa, sendo assim temos que:
Sabemos que
substituindo, teremos que:
Agora só precisamos determinar os valores de y, sendo assim teremos que ver o próximo passo.
Passo 3
Determinando o valor de y, temos que:
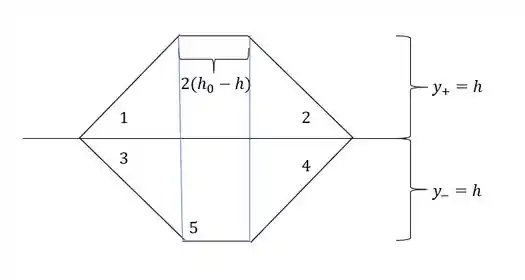
E podemos usar:
Calculando a tensão teremos que:
Passo 3
Para termos o valor de h para que a máxima tensão seja a menor possível, precisamos usar o nosso conceito de modulo de resistência. Isso ocorre porque o cálculo da tensão é dado pela seguinte equação:
Onde:
Se queremos que o valor da tensão seja o menor possível, temos que ter que o modulo resistente tem que ser o maior possível, sabemos que para situação final temos que:
Como queremos que o valor do módulo resistente seja máximo, basta derivarmos ele e igualarmos ela a zero.
tendo o valor de h que causa o máximo módulo resistente e consequentemente a menor tensão final, podemos determinar agora o valor dessa tensão em função da altura inicial, sendo assim teremos que:
Substituindo na fórmula de tenções, teremos que:
E também já determinamos o valor da tensão inicial, sendo assim teremos que:
E pela equação dada no enunciado temos que: