Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas - Ex. 121
Usando um computador e funções degrau, calcule a força cortante e o momento fletor para a viga e o carregamento mostrados. Use o incremento especificado, começando no ponto A e terminando no apoio direito.
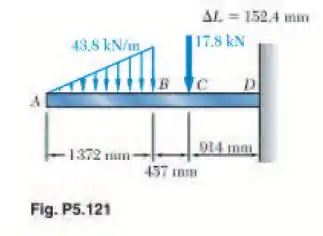
Passo 1
Beleza! A primeira coisa que vamos fazer é desenhar o diagrama de corpo livre para a viga, dessa forma, o DCL será:
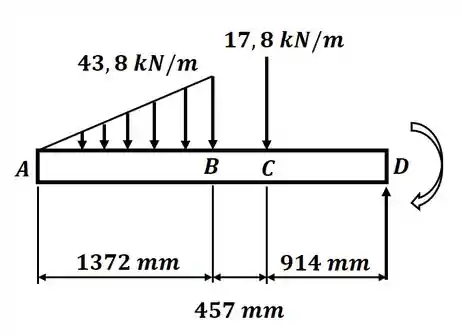
Nesse caso não precisamos nos preocupar em encontrar o valor da reação e do momento em D, pois para o cálculo das funções de singularidade, vamos adotar como referência de origem o ponto A, dessa forma, o que temos no final da viga não iremos usar.
Agora, lembrando que, como temos carregamento distribuído que não vai até o final da viga (o carregamento triangular), devemos adicionar um outro carregamento, de mesma intensidade, mas sentido oposto, da posição em que o carregamento atual termina, até o final da viga. Além de prolongar o carregamento existente até o final da viga também. Sendo assim, o carregamento equivalente será:
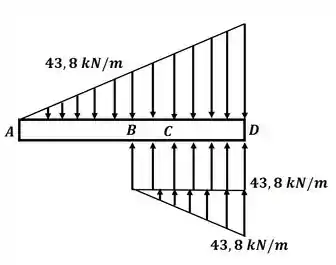
Agora podemos escrever o carregamento distribuído, considerando o ponto A como origem do nosso sistema, teremos:
Passo 2
Agora podemos encontrar a força cortante sabendo que ela será o oposto da integral da equação do carregamento, ou seja:
Substituindo a expressão para e resolvendo a integral, chegamos em:
A constante de integração nesse caso corresponde as forças localizadas aplicadas no sistema, no nosso caso, temos somente a força de 17,8 kN aplicada em C, então nossa constante será:
Então, nossa equação para a força cortante será:
Passo 3
Agora, para encontrarmos a equação do momento fletor, como já temos a equação para a força cortante, basta lembrar que a derivada do momento equivale a força cortante, ou seja:
Isolando as variáveis dessa equação, temos:
Integrando essa expressão dos dois lados, teremos:
Agora, substituindo a expressão encontrada para no passo 1, a equação acima se torna:
Resolvendo a integral, teremos:
Em que é a constante de integração. Nesse caso, a constante de integração corresponde aos momentos localizados que são aplicados ao sistema, no nosso caso não temos nenhum momento localizado, então teremos:
Então a equação do momento será:
Passo 4
Agora, com o auxílio do computador, calculando o valor da força cortante e do momento fletor em cada um dos pontos, começando de com incremento de , teremos a seguinte tabela de valores:
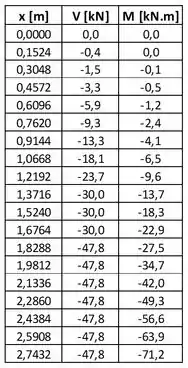
É isso aí! O exercício acabou aqui! O enunciado não pede, mas vale a pena observar na tabela onde temos o maior valor para a força cortante e para o momento fletor para entender a influência do carregamento dado.
Resposta
Ei, a resposta está no passo a passo :)