Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 49
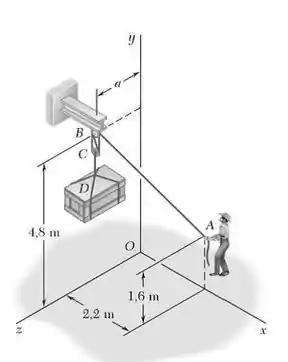
49. Para erguer um caixote pesado, um homem utiliza uma talha presa embaixo de uma viga pelo gancho . Sabendo que os momentos em relação aos eixos e da força exercida em pela porção da corda são, respectivamente, e , determine a distância .
Passo 1
Bom! A primeira coisa que temos que fazer é determinar a distância em termos dos vetores unitários e ; afinal é nesse segmento que o homem está aplicando a força. Para isso, basta observar a figura. Veremos que o ponto está nas coordenadas e o ponto encontra-se nas coordenadas . Com isso, para achar basta fazer a diferença entre as coordenadas de e as coordenadas de :
Passo 2
Achada o nosso vetor vamos obter o quanto vale a força de tração também em termos dos vetores unitários e . Para fazer isso basta multiplicar a força pela distância vetorial e dividir tudo pelo módulo de :
Passo 3
A questão já nos fornece os momentos em relação aos eixos e da força exercida em pela porção da corda. Ora bolas; talvez tenha um jeito de relacionar esses momentos já dados com a expressão geral do momento .
Para fazer isso, dado que temos , só falta agora o vetor posição que parte da origem de aplicação da força até a linha de ação inicial da força em . Essa belezinha é o vetor !! Sabendo que tem as coordenadas :
Como temos tudo que precisamos; só nos resta aplicar a definição de momento:
Onde temos que:
Vamos então, fazer o produto vetorial usando o determinante matricial:
Esse é o nosso momento resultante!!! Para obter os momentos em cada eixo; basta associar cada componente do momento com seu versor ao respectivo eixo coordenado; para o eixo ; para o eixo e para o eixo :
E como sabemos que os momentos em relação aos eixos e da força exercida em pela porção da corda são, respectivamente, e ; basta usar a seguinte relação a seguir: