Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 4.Problemas - Ex. 51
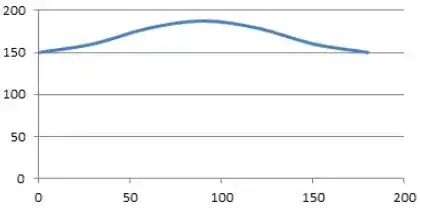
Usando uma chave para abrir rosca, a força de pode atuar no plano vertical em diversos ângulos . Determine a intensidade do momento que ela produz em relação ao ponto , faça um gráfico do resultado de (ordenada) versus (abscissa) para e especifique os ângulos que geram os momentos máximo e mínimo.
Passo 1
Vamos analisar essa questão.
Temos uma força que vai gerar um momento no ponto . Essa força vale e possui uma determinada angulação como mostrado na figura do enunciado.
Podemos então decompor essa força e aplicar o somatório de momento no ponto . Como a força está no plano podemos decompor em:
Para descobrir esse momento, podemos analisar de forma escalar ou vetorial. Observe o Exemplo 4.6 na página 115 do seu livro. Para problemas desse tipo, eu sempre gosto de trabalhar com o método de análise vetorial, pois fica mais fácil de não se perder. Temos que:
Passo 2
Portanto, temos que:
Resolvendo o determinante, temos que:
Podemos encontrar a sua magnitude:
Rearranjando, temos que:
Passo 3
No passo anterior encontramos uma equação para a magnitude de provocada pela força. Este momento depende de . Para encontrar o valor mínimo e máximo do momento vamos derivar e igualar a :
Este resultando será verdadeiro quando:
Como varia de a , temos que o valor máximo do momento será em e o valor mínimo será em .
Para o valor máximo, temos que:
Para o valor mínimo, temos que:
Passo 4
O exercício nos pede para fazer um gráfico de . Como nós temos a equação de que depende de podemos tabelar os dados e construir nosso gráfico:
Logo:
