Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 47
5.47. Determine the x- and y-coordinates of the centroid of the shaded area.
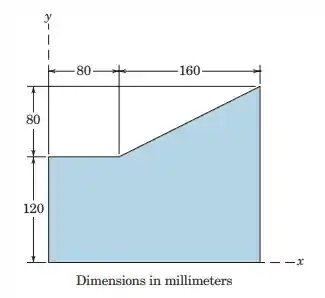
Passo 1
Para encontrar as coordenadas do centroide podemos usar as equações
Mas esse problema aqui vai simplificar as coisas para a gente, porque a densidade é homogênea. Então ficamos com
Passo 2
O raciocínio principal da questão é dividir a figura toda em duas figuras mais simples, desse jeito:
Agora a gente só tem que resolver para as figuras separadamente, vamos começar com o quadrado.
E a área do quadrado é
Então temos o primeiro ponto do que vamos considerar
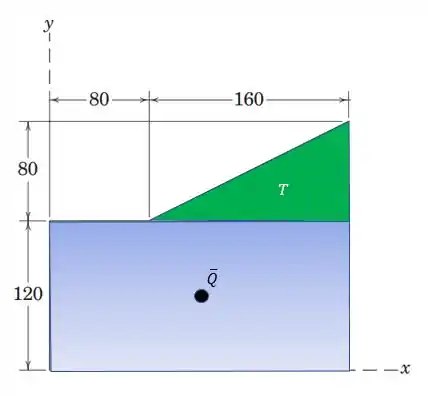
Passo 3
Agora vamos fazer para o triângulo . Para ficar mais simples, vamos mudar um pouco as coordenadas, vamos colocar o nosso centro na ponta do triângulo:
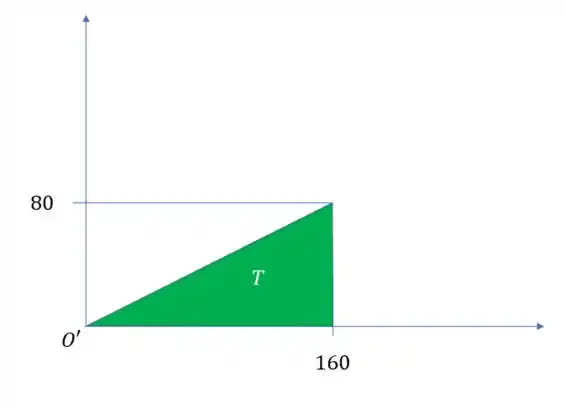
Agora vai ficar mais fácil calcular o centroide nesse sistema.
Agora vamos passar para os eixos de coordenadas originais, para fazer isso basta somar as coordenadas da nova origem .
E
Agora temos o centroide do triângulo
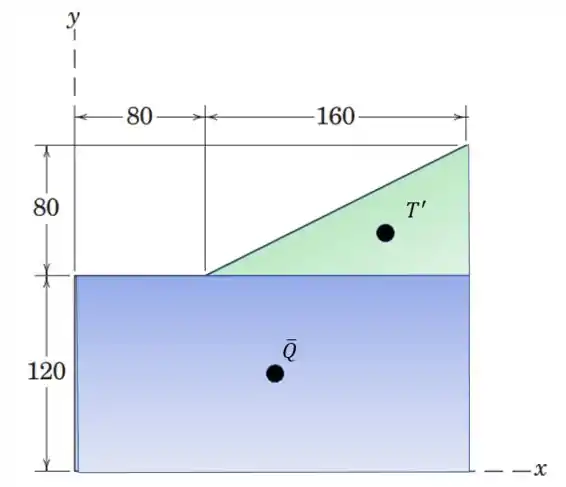
Só falta calcular a área desse triângulo:
Passo 4
Agora podemos finalmente usar a equação
E essa equação vira
Vamos substituir os valores na equação
E agora vamos fazer para o eixo
Substituindo os valores
Então o ponto do centroide é