Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 236
Determine o momento fletor máximo para a viga carregada e especifique a distância à direita da extremidade onde existe .
Passo 1
Fala galera, tudo certo? Bora fazer mais um exercício? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar o momento fletor máximo o qual a viga está submetida devido à carga distribuída triangular e a distância em relação ao ponto onde ocorre esse momento máximo.
Então bora lá! Para resolver esse problema, vamos começar analisando o diagrama de corpo livre:
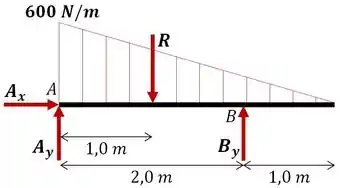
Onde a força distribuída triangular que inicia em pode ser substituída pela resultante que é dada por:
E está atuando a de , conforme mostrado.
Passo 2
Show de bola! Vamos começar então determinando as reações de apoio em e . Como não há nenhuma força externa horizontal aplicada, já temos de cara que:
Além disso, pela condição de equilíbrio da estrutura, podemos usar o somatório de momentos em torno de para determinar .
E fazendo o equilíbrio de forças na direção :
Passo 3
Tranquilo né? Bom, agora para descobrirmos o momento máximo na viga e o seu ponto de aplicação, precisamos das equações de cortante e momento da viga. Como no vão é onde ocorre a maior concentração de cargas, o momento máximo vai ocorrer nesse vão, logo, vamos nos atentar em fazer as equações para esse intervalo.
Entre os apoios e temos uma carga distribuída trapezoidal que inicia em e chega em com . O que é o mesmo que considerar uma carga distribuída constante de somada a uma carga distribuída triangular que inicia com em e chega em igual a . Logo, no apoio onde , a cortante é dada por:
E para uma posição qualquer, a equação da cortante é:
Onde a constante pode ser encontrada usando :
Passo 4
Agora ficou fácil né? Por definição, o momento máximo ocorre quando , logo:
Como o ponto onde ocorre o momento máximo deve estar entre e :
Passo 5
Ainda tem coisa pra fazer?
Calma que tá acabando! Hahaha
Até aqui nos descobrimos o ponto onde ocorre o momento máximo, para determinar o valor do momento a partir desse ponto precisamos da equação de momento da viga no intervalo , que pode ser obtida integrando a equação da cortante:
Uma vez que o momento máximo ocorre em :
É isso, galera. Até que foi tranquilo né? Partiu pra próxima!
