Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas - Ex. 47

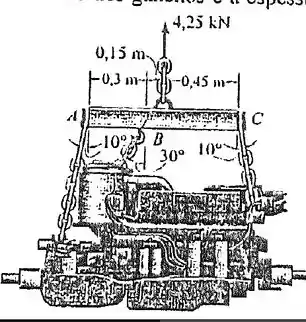
5.47. O motor possui um peso de 4,25   k N . Determine a força que cada corrente exerce sobre os ganchos em A, B e C. Despreze a dimensão dos ganchos e a espessura da viga.

Passo 1

Fala, querido! Queremos as forças em A , B e C . Vamos fazer um DCL para entender o que tá havendo:

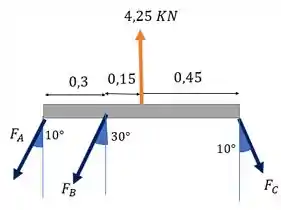
Aí a gente precisa usar as equações de equilíbrio para achar essas forças. Mas como elas estão inclinadas, vamos ter que decompor elas em y ou em x quando formos usar.

Bora!

Passo 2

Beleza, como o sistema está estático, podemos dizer que

∑ M B = 0

Considerando o sentido horário como positivo, e reparando que somente as componentes verticais das forças geram momento, temos:

∑ M B = F A ⋅ cos ⁡ 10 ° ⋅ 0,3 + 4250 ⋅ 0,15 - F C ⋅ cos ⁡ 10 ° ⋅ 0,6 = 0

Podemos dizer também que

F R y = 0

F R y = 4250 - F A ⋅ cos ⁡ 10 ° - F B ⋅ cos ⁡ 30 ° - F C ⋅ cos ⁡ 10 ° = 0

Por fim

F R x = 0

F R x = F C ⋅ sin ⁡ 10 ° - F B ⋅ sin ⁡ 30 ° - F A ⋅ sin ⁡ 10 ° = 0

Repara que os ângulos que orientam nossas forças estão colados no eixo vertical, isso quer dizer que ao decompor as forças, as componentes verticais ficam com cosseno e as horizontais com seno.

Passo 3

Agora temos três equações e três incógnitas. Vamos precisar resolver esse sisteminha linear.

F A ⋅ cos ⁡ 10 ° ⋅ 0,3 + 4250 ⋅ 0,15 - F C ⋅ cos ⁡ 10 ° ⋅ 0,6 = 0

4250 - F A ⋅ cos ⁡ 10 ° - F B ⋅ cos ⁡ 30 ° - F C ⋅ cos ⁡ 10 ° = 0

F C ⋅ sin ⁡ 10 ° - F B ⋅ sin ⁡ 30 ° - F A ⋅ sin ⁡ 10 ° = 0

Resolvendo essas equações, temos

F A = 2157,8   N

F B = 0

F C = 2157,8   N

Resposta

F A = 2157,8   N

F B = 0

F C = 2157,8   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os blocos D e E possuem uma massa de 4 kg e 6 kg, respectivamente. Se x = 2 m, determine a força F e a distância s para que haja equilíbrio.
Determine a rigidez kT da mola singular, de modo que a força F a estique pela mesma distância s que a força F estica as duas molas conjuntas. Expresse kT em termos da rigidez k1 e k2 das duas molas.
Se a mola DB possui um comprimento não esticado de 2 m, determine a rigidez da mola para manter o caixote de 40 kg na posição mostrada.
Uma esfera de 4 kg é apoiada em uma superfície parabólica lisa. Determine a força normal que ela exerce sobre a superfície e a massa mB do bloco B necessária para mantê-la na posição de equilíbrio mos
As molas BA e BC possuem uma rigidez de 500 N/m cada e um comprimento não esticado de 3 m. Determine a força horizontal F aplicada à corda que está presa ao pequeno anel B, de modo que o deslocamento