Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 56
56. No problema determine o momento sobre a diagonal exercida pela força na armação pela porção do cabo.
Passo 1
Bom! Antes de mais nada, vamos definir novamente a expressão de momento em relação a como sendo:
Esse , é porque nós queremos posicionar nosso sistema de referência em relação a diagonal . Para fazer isso basta escrever em termos do cosseno e do seno do ângulo , daquele triangulozinho que vemos na figura. Como o triângulo está no plano e claramente podemos ver que:
Então, tiramos que:
O termo que acompanha o eixo está negativo, porque caminhamos no sentido contrário do eixo, de para . Só para quem tiver alguma dúvida!!
Em seguida, a segunda coisa que temos que fazer é determinar a distância em termos dos vetores unitários e ; afinal esse segmento é o vetor posição . Para isso, basta observar a figura do enunciado. Veremos que o ponto está nas coordenadas em metros e o ponto, encontra-se nas coordenadas . Com isso, para achar basta fazer a diferença entre as coordenadas de e as coordenadas de :
Passo 2
Achada o nosso vetor , vamos olhar a figura novamente. Vamos tratar de decompor a força de tensão presente no cabo :
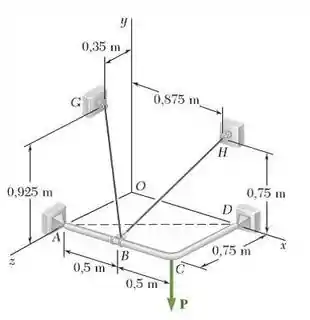
Para fazer isso, determinemos a distância vetorial em termos dos vetores unitários e . Só nos resta então, observar a figura do enunciado. Veremos que o ponto está nas coordenadas em metros e o ponto, encontra-se nas coordenadas . Com isso, para achar , basta fazer a diferença entre as coordenadas de e as coordenadas de:
E precisamos também do valor de , em módulo, né?
Desse jeito, a nossa tração vai ser dada por:
Passo 3
Por fim, apliquemos a definição de momento:
Onde temos que:
E vamos então, fazer o produto vetorial usando o determinante matricial:
Esse é o nosso novo momento resultante!!