Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas - Ex. 43
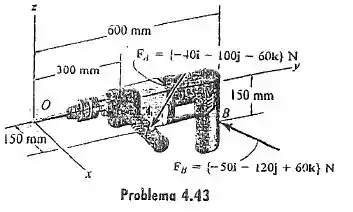
Determine o momento produzido por cada força em relação ao ponto localizado na broca da furadeira. Expresse o resultado como um vetor cartesiano.
Passo 1
Fala aí, bora resolver essa parada junto?
Para determinar o momento em seu vetor cartesiano, precisamos primeiramente determinar o vetor dito como comprimento.
Como assim vetor comprimento? Bem, temos um vetor que começa no ponto e vai até o ponto , ponto e precisamos determinar os vetores e .
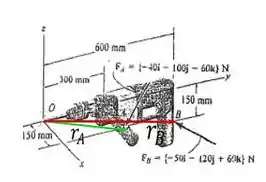
E ao determinar os vetores multiplicaremos pelas suas respectivas forças, resultando no momento causado por cada força.
Passo 2
Determinando o vetor , Vamos lá!
Note que na figura temos os eixos cartesianos, olhando para figura, podemos afirmar que as coordenadas do ponto é a seguinte:
Multipliquei cada ponto por para converte a unidade para .
E as coordenadas do ponto , fica o seguinte:
Considerando o ponto como inicial e o ponto como final do nosso vetor pode ser determinado, pela seguinte definição:
Substituindo os pontos, temos:
Passo 3
Vamos executar os mesmos passos feitos para o vetor , faremos para o vetor .
As coordenadas do ponto , olhando para figura, é o seguinte:
Multipliquei cada ponto por para converte a unidade para .
Considerando o ponto como inicial e o ponto como final do nosso vetor pode ser determinado, pela seguinte definição:
Substituindo os pontos, temos:
Passo 4
Temos os nossos vetores comprimento e vetor força, basta, para determinar o momento, efetuar a multiplicação vetorial. Pois, desejamos o momento na forma vetorial.
Executando o determinante teremos o nosso vetor :
Passo 5
Temos os nossos vetores comprimento e vetor força, basta, para determinar o momento, efetuar a multiplicação vetorial. Pois, desejamos o momento na forma vetorial.
Executando o determinante teremos o nosso vetor :