Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas - Ex. 48
48. A força age perpendicularmente ao plano inclinado. Determine o momento produzido por em relação ao ponto A. Expresse o resultado como um vetor cartesiano.
Passo 1
Para fornecer o resultado como o enunciado pede precisamos calcular o momento da força usando o produto vetorial que é dado da seguinte maneira:
Onde:
representam as coordenadas do vetor que vai da origem da rotação até o ponto de aplicação da força;
são as componentes da força aplicada.
O vetor mencionado acima pode ser visto na figura abaixo.
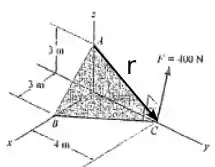
E esse vetor tem como coordenadas
Mas para usarmos esse método temos que expressar a força como um vetor cartesiano, e como fazemos isso?
É simples, basta multiplicar o módulo da nossa força pelo vetor direção da mesma. Esse vetor direção nada mais é que um vetor unitário que aponta na mesma direção da força. Ele pode ser calculado da seguinte maneira:
Onde para o nosso caso pode ser qualquer vetor normal ao plano, já que qualquer vetor dessa forma terá a mesma direção do vetor da força. Mas para obter esse vetor perpendicular ao plano podemos fazer o produto vetorial entre e , faremos isso porque se lembrarmos, o produto vetorial entre dois vetores fornece um verto que é perpendicular ao pano dos vetores.
Passo 2
Vamos então fazer o produto vetorial entre e para obtermos o vetor perpendicular que queremos.
Esse vetor então é perpendicular ao plano da figura.
Agora calculando o vetor direção do da força, da maneira que foi mencionado acima.
Passo 3
Agora vamos achar nossa força expressa na forma de vetor cartesiano.
Passo 4
Agora já temos tudo para calcular o momento da força .
Resposta
O momento produzido pela força em A é: