Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 57
57. Resolva o Problema 9.2 usando o círculo de Mohr.
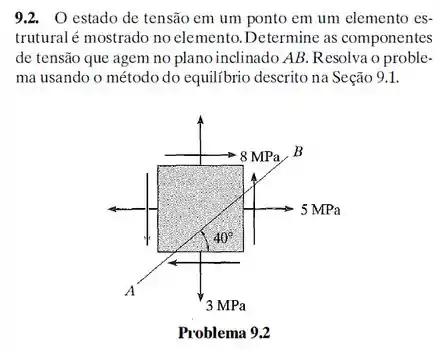
Passo 1
Fala, meu querido! Queremos as tensões que agem no plano . Se a gente girar o nosso elemento original no sentido anti-horário de , chegamos no estado de tensões pedido, porque a base do nosso elemento fica paralela a .
Precisamos então das tensões quando aplicamos esse giro em nosso elemento.
Da seguinte figura de estado plano, tiramos também que:
Ambas saindo das faces.
Positiva, porque as setas convergem para o 1° e 3° quadrante.
Bora lá montar nosso círculo de Mohr e matar essa questão!
Passo 2
Como estamos trabalhando com Círculo de Mohr, a primeira coisa a se fazer é determinar o centro do círculo, que é dado por:
Substituindo os valores numéricos correspondentes, chega-se à:
E em seguida, vamos determinar o raio do nosso círculo, através da fórmula da tensão de cisalhamento máximo:
Trocamos as variáveis pelos seus respectivos valores numéricos:
E vamos determinar as coordenadas e que representam nosso estado de tensões:
Agora temos tudinho!
Passo 3
Vamos montar nosso círculo
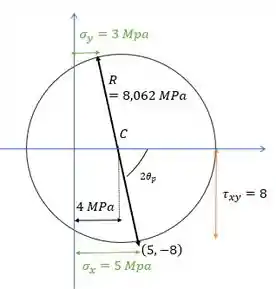
Vamos achar o ângulo que caracteriza o nosso estado. Pela figura, vemos que dá para fazer:
E como a gente chega no estado de tensões que ele pediu girando nosso elemento no sentido anti-horário, para gente chegar nele no circulo de Mohr, precisamos girar duas vezes esse ângulo no sentido anti-horário.
Ou seja, vamos girar nosso segmento que representa o nosso elemento no sentido anti-horário.
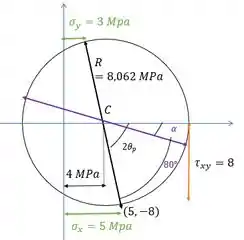
E aí o ângulo que nosso novo elemento faz com a horizontal é:
Passo 4
Aí a gente consegue achar as tensões para esse novo elemento pelo nosso círculo
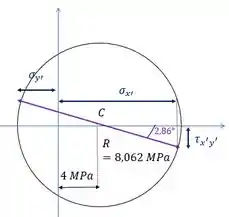
Por relação trigonométrica, dá pra saber que:
E como temos os valores:
Susbstituímos nas duas fórmulas anteriores das tensões:
Alcançamos nosso resultado:
Obs: temos algumas diferenças para o gabarito. Mas tá tudo certinho.