Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 67
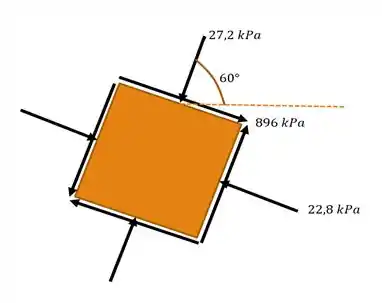
67. Determine o estado de tensão equivalente se um elemento estiver orientado a em sentido anti-horário em relação ao elemento mostrado. Mostre o resultado no elemento.
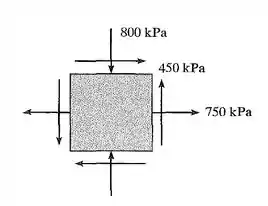
Passo 1
Da figura do enunciado, tiramos que:
Para construir o nosso famoso Círculo de Mohr a primeira coisa que temos que fazer é determinar o centro do círculo, que será dado através da fórmula da tensão média, , abaixo:
E substituindo os valores numéricos correspondentes, chegamos à:
Depois, a próxima coisa que temos que fazer é achar o raio do círculo através da fórmula da tensão máxima de cisalhamento, , que é dada por:
Trocando os valores de cada variável, obtemos nosso raio como:
Passo 2
Obtido o raio e o centro, já podemos construir o nosso círculo, que vai ter a seguinte cara da figura abaixo. Ah! Só lembrando aqui que nosso elemento está orientado de um ângulo de no sentido anti-horário, de modo que ele vai aparecer no nosso círculo com o dobro do seu valor, isto é, .
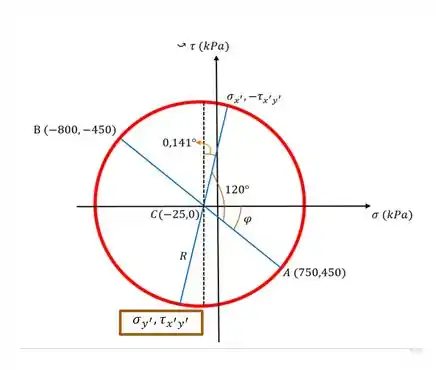
O próximo passo agora, é determinar o nosso ângulo , que se for olhar bem o círculo, é dado por:
E o nosso ângulo que queremos para realizar nossos cálculos é dado pela subtração abaixo, conforme dá pra ver no círculo de Mohr:
Passo 3
Agora, basta olhar o círculo novamente para encontrar as fórmulas de nossas tensões de estado plano, que são dadas por:
Substituindo os valores numéricos pertinentes, chegamos à:
E aqui está o resultado:
Pra não perder a viagem, vamos fazer também fazer o esboço de nosso querido elemento né; que vai ter a seguinte aparência:
