Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.4 - Ex. 71
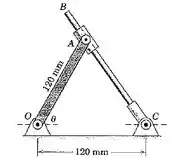
5/71) A barra desliza através do cursor articulado fixado à barra . Se possui uma velocidade angular no sentido horário de , determine a velocidade angular da barra quando .
Passo 1
Então galera , seja um ponto na barra coincidente com para
Onde ,
Passo 2
Bom pessoal , analisando a trigonometria do triângulo indicado na figura do enunciado , obtemos que :
E para acharmos a velocidade angular , por sua vez , basta aplicarmos a relação :
Resposta
Exercícios de Livros Relacionados
15. Se o centro O da roda está se deslocando com uma velocidade v 0 = 6 m / s , determine a velocidade do ponto A na roda. A cremalheira B está fixa.
14. Determine a velocidade angular do membro BC e a velocidade do pistao C no instante mostrado.
16. Se o cabo AB é desenrolado com uma velocidade de 3 m/s, e a cremalheira C tem uma velocidade de 1,5 m/s, determine a velocidade angular da engrenagem e a velocidade de seu centro O.
Resolva o Problema 16.58 utilizando o método do centro instantâneo de velocidade nula.
Resolva o Problema 16.54 utilizando o método do centro instantâneo de velocidade nula.