Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.4 - Ex. 65
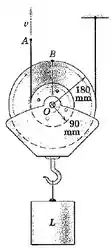
5/65) As duas polias são rebitadas em conjunto para formar uma única unidade rígida , e cada um dos dois cabos está firmemente enrolado em torno de suas respectivas polias . Se o ponto no cabo de elevação possui uma velocidade , determine os módulos da velocidade do ponto e da velocidade do ponto da polia maior para a posição mostrada .
Passo 1
Então galera , analisando a trigonometria do triângulo indicado a figura do enunciado , obtemos que :
Logo ,
Passo 2
Além disso , pelas relações aprendidas neste capítulo , sabemos que :
Assim como :
Sendo assim , temos que :
Portanto ,
Resposta
Exercícios de Livros Relacionados
5/77) A manivela O A oscila em torno da posição θ = 0 obrigando C B , por sua vez , a oscilar . Se O A possui uma velocidade angular no sentido anti-horário de 6r a d / s quando θ = 30 ° , determine a
5/70) O disco circular rola sem deslizar com uma velocidade angular no sentido horário ω = 4r a d / s . Para o instante representado , escreva as expressões vetoriais para a velocidade de A com relaçã
5/75) Cada uma das barras deslizantes A e B se acopla na sua borda respectiva das duas rodas rebitadas sem deslizar . Determine o módulo da velocidade do ponto P para a posição indicada.
5/72) No instante representado , a velocidade do ponto A da barra de 1,2m é de 3m / s para a direita . Determine a velocidade v B do ponto B e a velocidade angular ω da barra . O diâmetro das pequenas
5/73) A unidade em A consiste em um motor com redução de alto torque que gira a barra A B na taxa constante θ ' = 0,5r a d / s . A unidade A é livre para se mover ao longo da superfície horizontal . D