Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.5 - Ex. 25

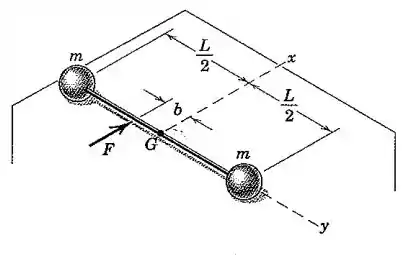
Duas esferas de aço, cada uma com massa m , estão soldadas a uma haste leve de comprimento L e massa desprezível e estão inicialmente em repouso sobre uma superfície horizontal lisa. Uma força horizontal de módulo F é subitamente aplicada à haste conforme indicado. Determine

(a) a aceleração instantânea a - do centro de massa G e

(b) a taxa correspondente θ ¨ em que a velocidade angular do conjunto em torno de G está variando com o tempo.

Passo 1

(a) Lembre-se de que, pela Segunda Lei de Newton:

∑ F x = ∑ m i a - x

F = 2 m a -

a - = F 2 m

Passo 2

(b) O módulo H G da quantidade de movimento angular em torno do centro de massa G é dado por:

H G = ∑ m i r i v i = ∑ m i r r θ ˙ = 2 m r 2 θ ˙ = 2 m L 2 2 θ ˙

H G = 1 2 m L 2 θ ˙

Derivamos essa equação em relação ao tempo:

H ˙ G = 1 2 m L 2 θ ¨

Passo 3

Por último, vamos lembrar da seguinte equação:

∑ M G = H ˙ G

Como F é a única força realizando torque, aplicada a uma distância b do centro de massa G , temos:

F b = H ˙ G

F b = 1 2 m L 2 θ ¨

θ ¨ = 2 F b m L 2

Resposta

(a) a - = F 2 m

(b) θ ¨ = 2 F b m L 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas crianças, A e B, cada uma tendo uma massa de 30 kg, estão sentadas na borda do carrossel que gira a ω = 2r a d / s . Excluindo as crianças, o carrossel tem uma massa de 180 kg e um raio de giraçã
Uma pessoa que passa através da porta giratória exerce uma força horizontal de 90N em um dos quatro painéis da porta e mantém o ângulo de 15° constante em relação a uma linha que é normal ao painel. S
O centro de massa G da barra esbelta de massa 0,8k g e comprimento 0,4m está caindo verticalmente com uma velocidade v = 2m / s no instante representado. Calcule a quantidade de movimento angular H o
O volante de 75k g tem um raio de giração em relação à linha de centro do seu eixo de k - = 0,5m e é submetido ao torque M = 10 1 - e - t N . m , onde t é expresso em segundos. Se o volante está em re
O centro de massa G da barra esbelta de massa 0,8k g e comprimento 0,4m está caindo verticalmente com uma velocidade v = 2m / s no instante representado. Calcule a quantidade de movimento angular H o