Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.5 - Ex. 70

70- Substitua a rosca quadrada do macaco da Fig.6/6 pela rosca em V como indicado na figura que acompanha esse problema e determine o momento M no parafuso necessário para levantar a carga W . A força R   atuando em uma pequena seção representativa da rosca está mostrada, com suas projeções relevantes. O vetor R 1 é a projeção de R no plano da figura que contém o eixo do parafuso. A análise é iniciada com um somatório da força axial e dos momentos e inclui substituições para os ângulos γ e β em termos de θ , α e do ângulo de atrito ϕ = tan - 1 ⁡   μ . O ângulo de hélice da rosca simples está exagerado para melhor visualização.

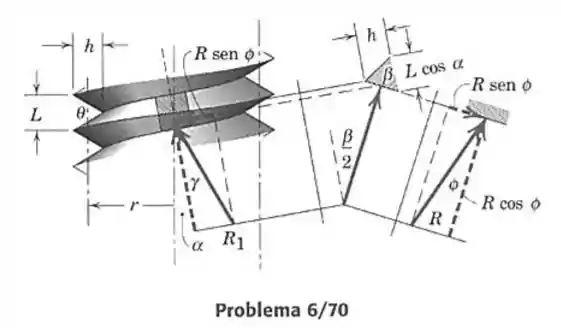
Passo 1

O equilíbrio na direção axial no problema será:

∑ F = 0 → W = ∑ R c o s α + γ = c o s ⁡ ( α + γ ) ∑ R 1

Onde W é a carga axial que o parafuso precisamos suportar e fazendo o cosseno de todas as cargas R 1 no parafuso serão a reação a essa carga W .

Já o momento assim como na rosca quadrada será:

∑ M = 0 → M = ∑ R 1 r sin ⁡ α + γ = r sin ⁡ α + γ ∑ R 1

Passo 2

Combinando as duas equações temos:

M W = r t a n ( α + γ )

M = W r   t a n ⁡ ( α + γ )

Porém a relação trigonométrica de soma de ângulos em uma tangente é dada por:

t a n a + b = tan ⁡ a + tan ⁡ b 1 - t a n   a   tan ⁡ b

Logo:

M = W r × tan ⁡ α + tan ⁡ γ 1 - t a n α tan ⁡ γ

Porém da figura conseguimos ver que:

tan ⁡ γ = x y = R   s e n   ϕ y

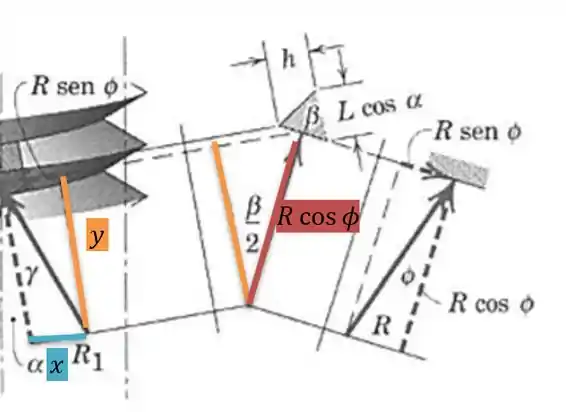
Porém do triângulo retângulo a direita conseguimos ver que:

x = R c o s   ϕ cos ⁡ β

Logo:

tan ⁡ γ = R sen ⁡ ϕ R cos ⁡ ϕ cos ⁡ β 2

Ou:

tan ⁡ γ = μ cos ⁡ β 2

Passo 3

Da figura também conseguimos tirar dois triângulos:

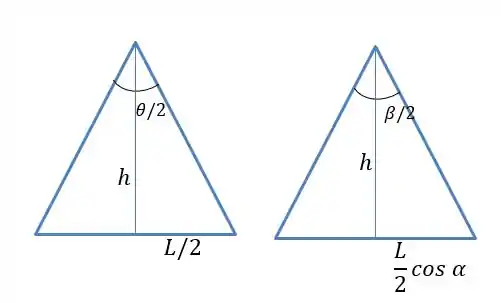
Logo temos as seguintes relações:

t a n θ 2 = L 2 h

t a n β 2 = L cos ⁡ α 2 h

Substituindo L 2 h da primeira equação para a segunda temos:

tan ⁡ β 2 = t a n θ 2 cos ⁡ α

Porém queremos saber o cosseno de β / 2 não a tangente, logo temos que aplicar a seguinte relação trigonométrica:

tan 2 ⁡ x + 1 = 1 cos 2 ⁡ x

Onde:

cos ⁡ x = 1 1 + tan 2 ⁡ x

Logo:

cos ⁡ β 2 = 1 1 + tan 2 ⁡ θ 2 cos 2 ⁡ α

Substituindo esse resultado teremos a tangente de γ .

t g γ = μ 1 + tan 2 ⁡ θ 2 cos 2 ⁡ α

O que nos dá a monstruosa equação de momento:

M = W r × tan ⁡ α + μ 1 + tan 2 ⁡ θ 2 cos 2 ⁡ α 1 - t a n α μ 1 + tan 2 ⁡ θ 2 cos 2 ⁡ α

Onde α é o mesmo α da rosca quadrada :

tan ⁡ α = L 2 π r

Resposta

M = W r × tan ⁡ α + μ 1 + tan 2 ⁡ θ 2 cos 2 ⁡ α 1 - t a n α μ 1 + tan 2 ⁡ θ 2 cos 2 ⁡ α

Onde:

α = tan - 1 ⁡ L 2 π r

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No sacador de engrenagensmostrado na figura, o parafuso de rosca quadrada A B tem um raio médio de 15m m e um avanço de 4m m . Sabendo que o coeficiente de atrito estático é 0,10 , determine o torque
No sacador de engrenagensmostrado na figura, o parafuso de rosca quadrada A B tem um raio médio de 15m m e um avanço de 4m m . Sabendo que o coeficiente de atrito estático é 0,10 , determine o torque
No sacador de engrenagensmostrado na figura, o parafuso de rosca quadrada A B tem um raio médio de 15m m e um avanço de 4m m . Sabendo que o coeficiente de atrito estático é 0,10 , determine o torque
Na morsa de bancada mostrada, o mordente móvel D está rigidamente ligado a lingueta A B que se encaixa com folga no corpo fixo da morsa. O parafuso de rosca simples é rosqueado na base fixa e tem um d
Considerando no Problema 8.70 que uma rosca à direita seja usada em ambas as barras A e B , determine a intensidade do torque que deve ser aplicado à luva a fim de girá-la.