Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas - Ex. 77
77. A placa possui um peso com centro de gravidade em . Determine a distância ao longo da linha onde a força vertical fará com que a tração no fio seja zero.
Passo 1
Primeiro temos que avaliar que tipos de conexões temos nessa situação, nesse caso são três cabos, segundo a tabela do capítulo , seção , esse tipo de conexão por cabo só exerce uma força ou tração na direção do cabo.
Para facilitar nossa vida em um momento, vamos definir um novo eixo que passa pela força e o ponto , pois quando formos usar a equação de equilíbrio em relação a esse eixo, nem a força peso da placa e nem a força irão colaborar para o momento.
Abaixo temos um diagrama de corpo livre que vai nos ajudar a ver o que está acontecendo.
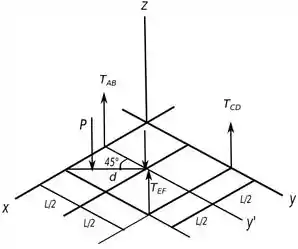
Agora só temos que aplicar as equações de equilíbrio para achar as forças que queremos.
O macete é sempre começar com as equações que te oferecem menos incógnitas.
Passo 2
Vamos primeiro usar a equação de equilíbrio referente ao momento em relação ao eixo .
O termo é a distância projetada no eixo que contribui para expressar a distância perpendicular de ao eixo , para o cálculo do momento.
Por enquanto vamos deixar assim, agora vamos atrás de outa equação que nos ajude.
Passo 3
Vamos então calcular o momento em relação ao eixo e vamos ver o que nos fornece.
O termo é a distância projetada no eixo que contribui para expressar a distância perpendicular de ao eixo , para o cálculo do momento.
Passo 4
Agora temos as seguintes equações:
Isolando na primeira equação e substituindo na segunda, temos:
Resposta
Ei, a resposta está no passo a passo :)