Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 5.Problemas - Ex. 79
A plataforma tem massa de 2 Mg e centro de massa localizado em G. Se ela for elevada com velocidade constante usando três cabos, determine a força em cada um dos cabos. Resolva para cada força usando uma única equação de equilíbrio dos momentos.
Passo 1
Oi, tudo bem? Vamos analisar esta questão.
O diagrama de corpo livre da plataforma é dado por:
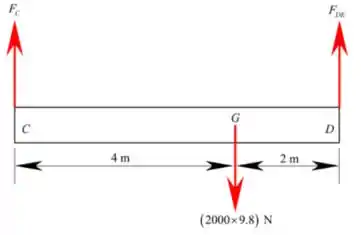
Fazendo o somatório de momento em , temos que:
Aplicando o equilíbrio das forças ao longo de , temos que:
Passo 2
Temos então a seguinte configuração para os cabos:
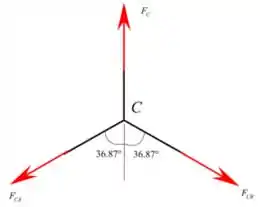
Aplicando o somatório de forças em , temos que:
Temos também que:
Resposta
Exercícios de Livros Relacionados
Determine a tração desenvolvida nos três cabos necessária para suportar o semáforo, que tem uma massa de 20 kg. Considere h = 3,5 m.
A luminária tem massa de 15k g e é suportada por um poste A O e cabos A B eA C . Se a força no poste atua ao longo de seu eixo, determine as forças em A O ,A BeA C para que haja equilíbrio.
Se cada uma das cordas se romper quanto estiver sujeita a uma tração de 450N , determine aforça de suspensão máxima F que atua no balão na iminência de que qualquer uma das cordas seja rompida.
Determine a tração desenvolvida nos três cabos necessária para suportar o semáforo, que tem uma massa de 15 kg. Considere h = 4 m.
A caixa de 150N é sustentada pelos cabos AB, AC e AD. Determine a tração nesses cabos.