A barra uniforme, de comprimento e peso , está apoaida na extremidade por uma parede lisa e na extremidade por uma corda de comprimento , que é presa à parede como mostra a figura. Mostre que , para o equilíbrio, é necessário que .
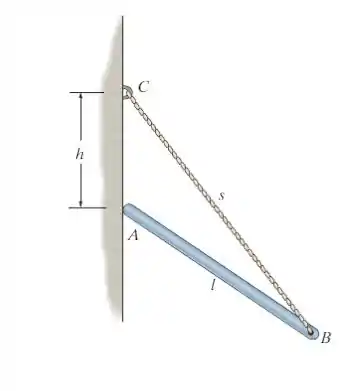
Passo 1
Em toda questão de mecânica geral nós sempre devemos desenhar o diagrama de corpo livre da situação para entendermos quais são as forças e componentes envolvidas. Para essa questão, temos o seguinte diagrama:
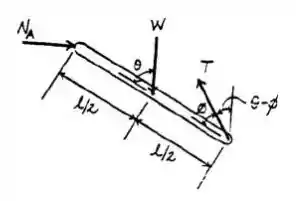
Passo 2
Galerinha, o valor da tensão na corda pode ser obtido diretamente da soma dos momentos em relação ao ponto . Como estamos numa situação de equilíbrio, a soma dos momentos em relçaão ao ponto tem que ser igual a zero. Assim, assumindo que o sentido anti-horário é positivo para o momento, temos:
Passo 3
Vamos ver o resultante vertical. Numa situação de equilíbrio, a soma de todas as forças que atuam na vertical tem que ser zero. Vamos assumir a direção para cima como positiva. Logo,
Vamos agora relembrar um pouquinho de geometria plana! Vocês lembram lá da lei dos Senos?? Se temos um triângulo qualquer , podemos escrever a seguinte relação:
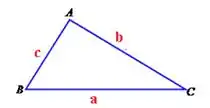
Vamos olhar pra nossa situação agora. Nós temos um triângulo formado pela corba, pela barra e pela parede em que a barra está enconstada, não temos? Fica mais ou menos assim:

Aplicando a lei dos senos para esse triângulo, temos:
O seno de pode ser escrito como . Assim,
Substituindo na expressão derivada do somatório de forças na vertical, temos:
Passo 4
Se usarmos a lei dos cossenos no triângulo do nosso problema, teremos:
Resposta
Ei, a resposta está no passo a passo :)