Exercícios de Equilíbrio em Três Dimensões - Lista de Exercícios Resolvida
Questão 1
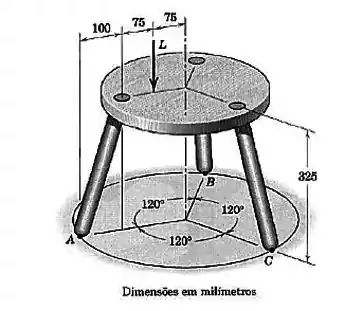
Uma banqueta de três pernas está submetida à carga , como mostrado. Determine a força de reação vertical sob cada perna. Despreze o peso da banqueta.
Questão 2
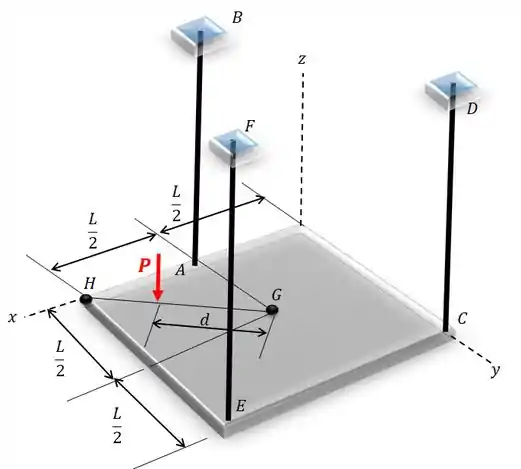
A placa possui um peso com centro de gravidade em . Determine a tração desenvolvida nos fios , e se a força é aplicada em .
Questão 3
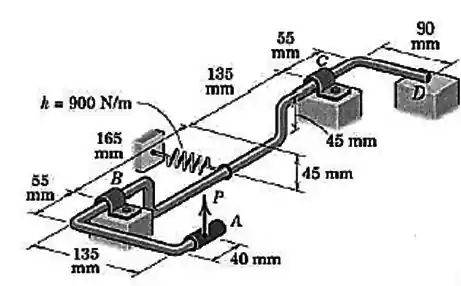
A mola de módulo é esticada de uma distância quando o mecanismo está na posição mostrada. Calcule a força necessária para iniciar rotação em torno do eixo e determine os módulos correspondentes das forças nos mancais, as quais são perpendiculares à . Qual é a força de reação normal em se ?
Questão 4
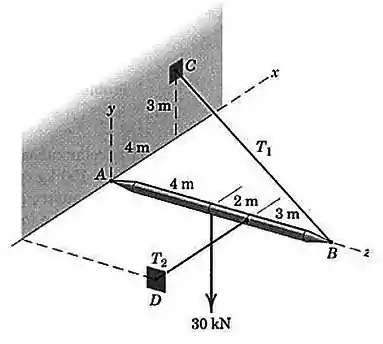
Se o peso do mastro é desprezível comparado à carga de aplicada, determine as forças trativas e nos cabos e a força atuando na rótula em .
Questão 5
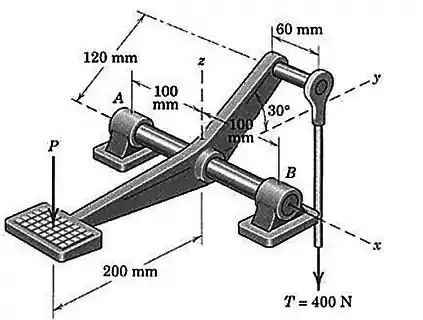
Uma força vertical no pedal do dispositivo é necessária para produzir uma força trativa de na barra de controle vertical. Determine as reações correspondentes nos mancais em e .
Questão 6
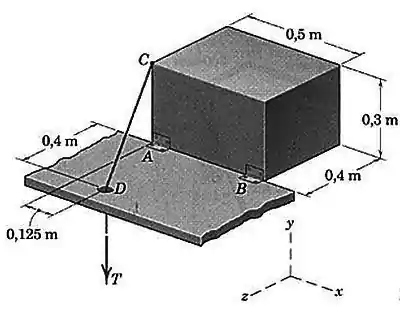
Determine a força trativa necessária para manter o sólido retangular na posição mostrada. O sólido retangular com é homogêneo. O atrito em é desprezível.
Questão 7
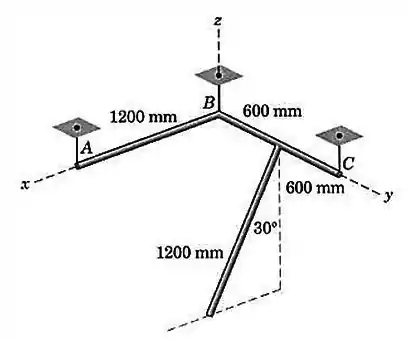
Cada uma das três barras uniformes de tem uma massa de . As barras estão soldadas juntas na configuração mostrada e estão suspensas por três arames verticais. As barras e estão no plano horizontal e a terceira barra está em um plano paralelo ao plano .Calcule as forças trativas em cada arame.
Questão 8
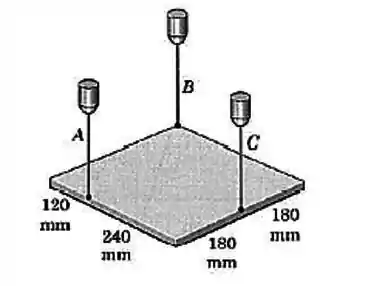
Uma chapa quadrada e uniforme de aço de de comprimento de aresta e uma massa de está suspensa no plano horizontal pelos três fios verticais, como mostrado. Calcule a força trativa de cada fio.
Questão 9
A porta retangular de acesso com é mantida na posição aberta, a , pelo apoio simples . Determine a força no apoio e o módulo da força normal ao eixo de abertura em cada pequena dobradiça e . Considere que na dobradiça a força horizontal e paralela à parede seja nula.
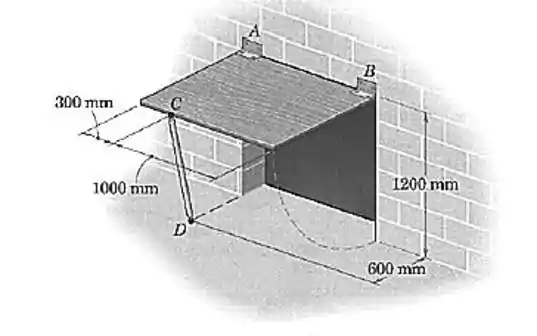
Questão 10
O eixo horizontal de aço tem uma massa de e está suspenso por um cabo vertical em e por um segundo cabo que passa por baixo do eixo e está situada em um plano vertical transversal. Calcule as forças trativas e nos cabos.
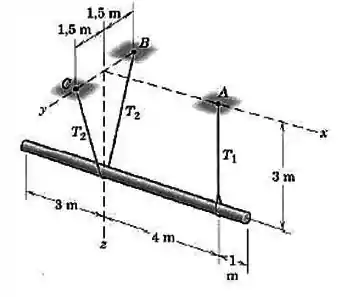
Questão 11
A estrutura é usada para armazenar e desenrolar cabos. A massa combinada da estrutura, do corretel e do cabo é de com centro de massa em . Determine as forças normais nos quatro pés e ) se o cabo sai pela parte de cima do carretel e o cabo sai pela parte de baixo do carretel em seu ponto médio horizontal. O raio efetivo do carretel é de .
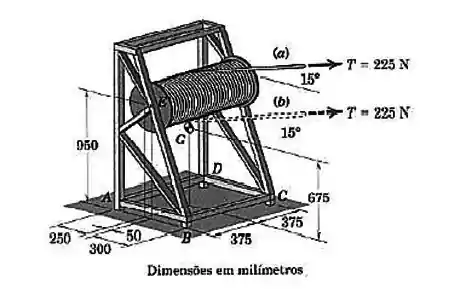
Questão 12
A parte de um lustre que é sustentada por correntes tem a forma de uma parte de casca esférica. Se a massa da parte de vidro é , determine a força trativa em cada uma da correntes.
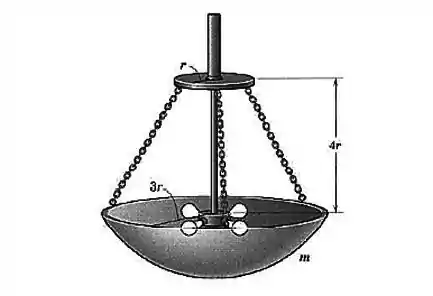
Questão 13
Determine o local e do ponto de aplicação da força de modo que a tração desenvolvida nos cabos , e seja a mesma. Despreze o peso da chapa.
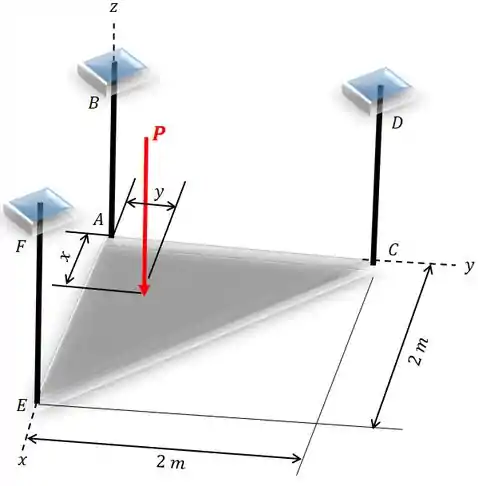
Questão 14
O mastro de , com centro de massa em , é mantido na posição mostrada por uma rótula em e por dois cabos e . Determine as forças trativas nos dois cabos e as componentes , e da força de reação em .
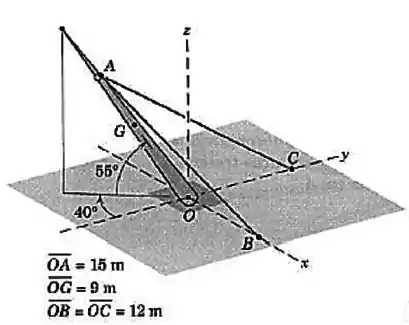
Questão 15
Durante um teste, o motor esquerdo do avião bimotor é acionado gerando um empuxo de . As rodas principais em e estão freadas de modo a evitar movimento. Determine a variação nas forças de reação normais e (comparativamente aos valores nominais com ambos os motores desligados).
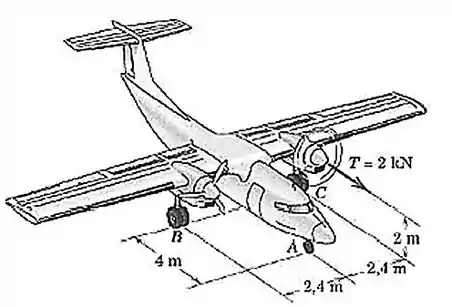
Questão 16
03) A placa quadrada , de lado e densidade superficial , está soldada a uma segunda placa quadrada de lado e densidade superficial . O centro conjunto é apoiado em e e articulado às barras de peso desprezível e , conforme indicado na figura. Sabendo-se que o peso da peça única constituída pelas duas placas homogêneas é e que o seu centro de massa se situa na posição , pede-se:
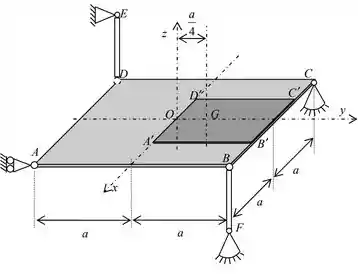
a) Determinar e em função de e dos demais dados fornecidos;
b) Desenhar os diagramas de corpo livre da placa e das barras;
c) Determinar, em função de , as reações nos apoios e e as forças nas barras e .
Ver solução completa