Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 10.Problemas - Ex. 100

σ c = 8,3   M P a e um módulo de elasticidade ajustado E = 11,1   G P a . Usando o método da tensão admissível, determine o maior comprimento de flambagem L admissível que pode ser usado.

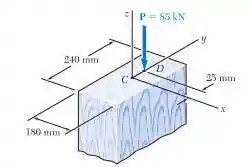
10.100: Resolva o Problema 10.99 considerando que P = 105 k N .

Passo 1

Então gurizada o enunciado pede que a gente determine o maior comprimento de flambagem L admissível que pode ser usado, então vamos trazer os dados do enunciado :D

E = 11,100 M P a           d = 180 m m = 0,180 m           b = 240 m m = 0,240 m

A = b d = 43,2 × 10 - 3 m 2           I x = 1 12 d b 3 = 1 12 0,180 0,240 3 = 207,36 × 10 - 6 m 4

e = 25 m m = 0,025 m     c = b 2 = 0,120 m

Passo 2

Agora vamos determinar a tensão :D

P A + P e c I ≤ σ a l l                   σ a l l ≥ 105 × 10 3 43,2 × 10 - 3 + 105 × 10 3 0,025 0,120 207,36 × 10 - 6 = 3,9496 × 10 6 P a = 3,9496 M P a

Defina y e x como

C p = σ a l l σ C = 3,1973 8,3 = 0,38522 = y           x = σ C E σ C

y = 1 + x 2 c - 1 + x 2 c 2 - x c   onde c = 0,8   “ f o r   s a w n   l u m b e r ”

1 + x 2 c - y = 1 + x 2 c 2 - x c

1 + x 2 c 2 - 1 + x c y + y 2 = 1 + x 2 c 2 - x c

1 + x 2 c - 1 + x c y + y 2 = 1 + x 2 c 2 - x c

x = y 1 - c y 1 - y = 0,47586 1 - 0,8 0,47586 1 - 0,47586 = 0,56227

Passo 3

Agora partiu determinar a largura :D

σ C E = σ C 0,56227 = 8,3 0,56227 = 4,6668 M P a

σ C E = K C E E L d 2             L 2 = K C E E d 2 σ C E             o n d e K C E = 0,300

L = d K C E E σ C E = 0,180 0,300 11,100 4,6668                                           L = 4,81 m

Resposta

4,81 m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

x a uma distância e do eixo geométrico. Sabendo que σ a d m = 75 M P aeE = 200 G P a , determine o maior comprimento L admissível quando (a) e=5mm e (b) e =12mm
W 200 × 35,9 que está livre na parte superior C e engastada na base B. Sabendo que a excentricidade da fora é e = 6,35 m m , determine o maior comprimento L admissível se a tensão admissível na coluna
10.54. Resolva o problema 10.53 considerando que a força axial de 53,4kN será aplicada à barra com uma excentricidade e = 1 2 d . 53,4 k N é aplicada com uma excentricidade e = 9,53 m m à barra circul
10.44: Resolva o Prob. 10.43 assumindo que o comprimento do tubo é aumentado para 5m. σ Υ = 250 M P a e E=200GPa. Sabendo que é exigido um fator de segurança de 2,6 com relação à deformação permanente
50 k i p s é aplicada a um ponto localizado no eixo x a uma distância e = 0,25 i n . Do eixo geométrico da coluna de aço BC de perfil laminado W * × 28 . Sabendo que a coluna é livre no seu topo C e f