Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 88
88- Uma haste uniforme de comprimento está apoiada dentro de um recipiente semiesférico de raio tal como mostra a figura. Desprezando o atrito, determine o ângulo correspondente a condição de equilíbrio.
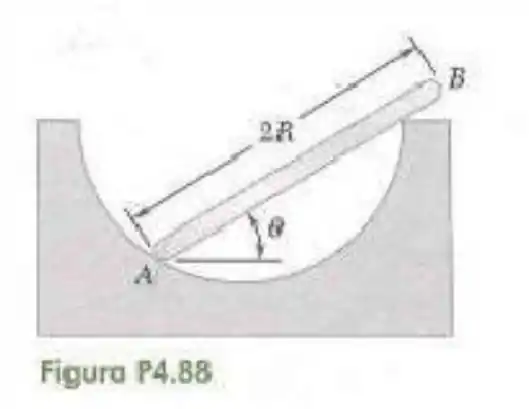
Passo 1
A reação em aponta para o centro do círculo pois todo raio de um círculo é normal a superfície circular. Já como um pouco antes de vem uma quina apenas podemos dizer que a força é perpendicular a barra a essa força vamos dar o nome de essas duas forças encontram-se exatamente acima do centro de gravidade da barra formando o seguinte diagrama de forças desenhado abaixo.
Passo 2
Agora vem o problema geométrico da questão, para isso vamos dar nome aos pontos e as medidas que temos só de olhar para a figura.
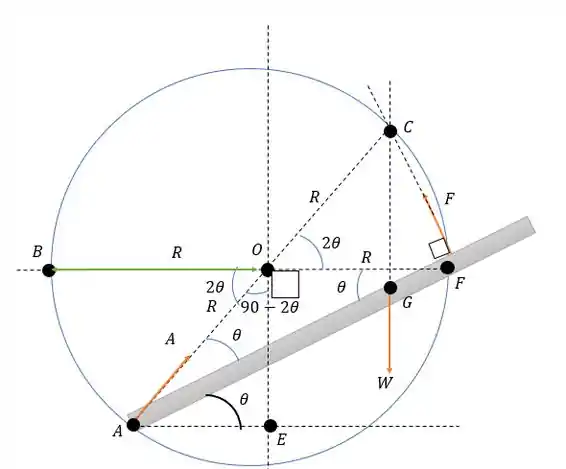
Eita ficou complexo, vamos dizer um roteiro de como achar isso tudo:
Foi nos dado que o ângulo vale
Logo pela propriedade dos ângulos também valerá
Por termos um triângulo isósceles então será
Isso fará com que pra que some valha porém o ângulo do quarto quadrante vale logo será
Para que dê graus no terceiro quadrante vale
E finalmente por ser ângulo oposto será
Acho que deu para ficar mais claro a imagem.
Passo 3
Mas espera pelo roteiro dado nós não utilizamos o ponto para nada (sem besteiras aqui) é aqui que nós iremos utilizar-lo (repito sem besteiras)
O comprimento de vale pois é a metade do comprimento da barra, enquanto vale como está exatamente abaixo de nós podemos rebater os dois na horizontal e conseguir a mesma distância e com isso nós iremos ter:
Porém e , logo:
Então:
Se fizermos nós teremos a seguinte equação do segundo grau:
Cujas raízes serão:
Ou seja temos dois ângulos iguais a:
Porém pelo nosso raciocínio é um ângulo agudo, sendo então a única resposta plausível.