Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 89

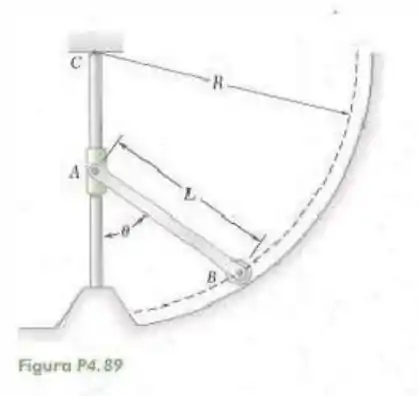
89- A haste delgada de comprimento L e peso W é presa a um cursor em A e equipada com uma pequena roda em B . Sabendo que a roda desliza livremente ao longo da superfície cilíndrica de raio R e desprezando o atrito, deduza uma equação com θ ,   L   e R que deve ser satisfeita quando a haste estiver em equilíbrio.

Passo 1

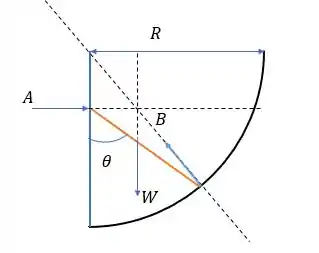
A reação em B para que fique normal a superfície será um vetor que aponta para o centro do círculo e para que A incercepte com o peso (que aponta sempre para baixo) A deverá estar na horizontal de forma que teremos o seguinte diagrama de forças.

Passo 2

Agora vamos resenhar o sistema para que consigamos extrair os ângulos que queremos:

Como o peso W está no centro da reta laranja então se rebatermos para horizontal e para a vertical nós teremos as seguintes distâncias L sin ⁡ θ   e L cos ⁡ θ , agora por semelhança dos triângulos C A V e C D B nós temos que:

x L 2 sin ⁡ θ = x + L c o s   θ L sin ⁡ θ

x = 1 2 x + L cos ⁡ θ 2

x = L cos ⁡ θ  

Passo 3

Agora vamos limpar nosso desenho e utilizar um triângulo que dê para correlacionar as três variáveis por Pitágoras ou lei dos cossenos:

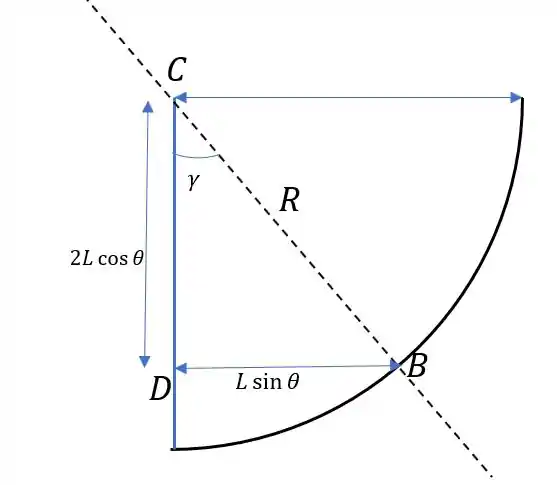
Por Pitágoras no triângulo D C B temos:

R 2 = 4 L 2 cos 2 ⁡ θ + L 2 sin 2 ⁡ θ

R 2 = 3 L 2 cos 2 ⁡ θ + L 2 cos 2 ⁡ θ + L 2 sin 2 ⁡ θ

R 2 = 3 L 2 cos 2 ⁡ θ + L 2

R 2 L 2 = 3 cos 2 ⁡ θ + 1

cos 2 ⁡ θ = 1 3 R 2 L 2 - 1

θ = cos - 1 ⁡ 1 3 R 2 L 2 - 1

Resposta

θ = cos - 1 ⁡ 1 3 R 2 L 2 - 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a figura abaixo (a) esboçe a tração no cabo em termo de θ e W e (b) determine o valor de θ tal que a tração vale 3W.
Desprezando o peso da barra AB, determine (a) a equação que deve ser satisfeita quando a haste está em equilíbrio e (b) determine o ângulo para equilíbrio quando P = 64 N ,Q = 48 N ,l = 500 m m e a =
O suporte A B C pode ser apoiado das oito diferentes maneiras mostradas nas figuras. Todas as conexões consistem em pinos sem atrito, roletes ou hastes curtas. Em cada caso, responda às questões apres
Resolva o Problema 6.161 considerando que o braço da cruzeta presa ao eixo C F é vertical.
Dois eixos A C e C F , que estão no plano vertical x y , estão acoplados por uma junta universal em C . Os mancais em B e D não exercem nenhuma força axial. Um binário de intensidade 50N ⋅ m (no senti