Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 90
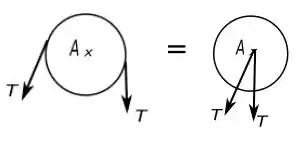
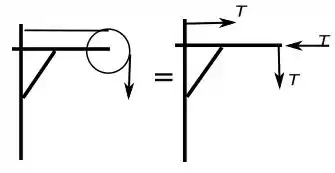90. Mostre que, quando uma estrutura sustenta uma polia em , um carregamento equivalente da estrutura e de cada uma de suas partes componentes pode ser obtido removendo-se a polia e aplicando-se em duas forças iguais e paralelas às forças que o cabo exerce na polia. Mostre que, se uma extremidade do cabo é presa na estrutura no ponto , uma força de intensidade igual à tração no cabo deve também ser aplicada em .
Passo 1
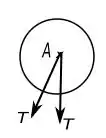
Primeiro temos que verificar que para uma polia lisa e sem atrito e imóvel, a tenção em toda corda continua a mesma, valos mostrar isso com a equação de equilíbrio referente à o momento em relação ao centro de uma polia, abaixo temos uma figura para visualizarmos melhor.
Com siderando que a polia tem raio , temos:
Está verificado então, agora sabemos que as forças na imagem que o enunciado fornece é a mesma tanto de um lado da polia quanto do outro.
Agora para analisar a situação do enunciado, item , vamos lembrar de uma coisa que já aprendemos nos capítulos anteriores do livro, que é a substituição de uma força por um sistema de forças ou momentos que tenham o efeito equivalente e é isso que faremos.
Agora para analisar a situação do enunciado, item , vamos usar o que acabamos de comprovar acima ao nosso favor.
Passo 2
Se você observar a figura referente ao item poderá ver que cada força produz um momento em relação ao centro da polia e ao mesmo tempo atua no centro de massa da polia, que no caso fica no centro da polia puxando o mesmo para a direção de atuação.
Então cada força pode ser substituída por um momento ( é o raio da polia), o que muda é o sentido de rotação, e por uma força paralela a original, mas que atua no centro de massa. Abaixo temos uma figura que representa essa equivalência.
Passo 3
Agora, se você reparar na figura do passo os momentos produzidos por cada força estão em direções diferentes, logo eles se cancelam então ficamos com:
Está provado o que o enunciado pedia no item .
Passo 4
Vamos lembrar que para uma corda com massa desprezível a força de tração age igualmente em todos os pontos da corda e utilizando o que verificamos no passo , então temos o seguinte:
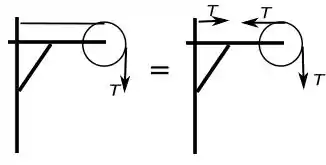
Então temos essa nova situação, se usarmos o que provamos no item paras forças na polia, ficamos com:
Está provado o que o enunciado pedia no item .
Resposta
