Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.6 - Ex. 95
95- Calcule a força de sustentação e o momento em A, para a viga em balanço carregada.
Passo 1
Como o ponto A é um engaste, temos 3 reações de apoio, vertical, horizontal e momento.
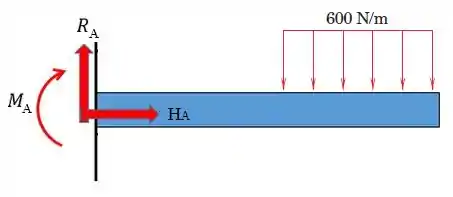
Mas como HA é a única força horizontal, ela vai ser nula, pelo somatório de forças horizontais.
Para fazer o somatório de forças verticais e o momento, vamos substituir a carga distribuída por uma força concentrada F. Essa força que tem que ficar no ponto central do intervalo onde a carga distribuída atua, ou seja, a 6m do ponto A. Sua magnitude é o produto do valor da carga pelo intervalo em que ela atua, ou seja:
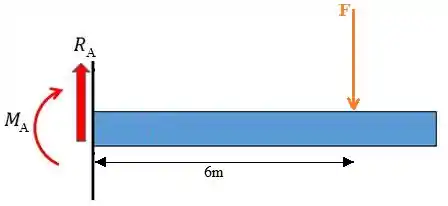
Pelo somatório de forças verticais, achamos RA:
Passo 2
Para encontrar o momento, fazemos o somatório de momentos no ponto A (sendo positivo o sentido horário). A força RA não faz momento em A, pois passa por esse ponto, e a força F tem o braço de alavanca igual a 6m.