Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.6 - Ex. 96

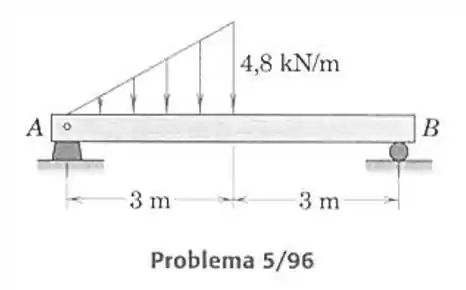
96- Calcule as reações em A e B para a viga submetida a carga distribuída triangular.

Passo 1

A carga triangular produz uma força resultante igual a área desse triângulo e ela é igual a:

A = 4.8   k N × 3 2 = 7.2   k N

E ela está localizada no centroide horizontal do triângulo, que está a 2 3 de distância do ponto A, que é:

2 3 × 3 = 2 m

Passo 2

Desenhando as forças de reação nos apoios A e B, teremos:

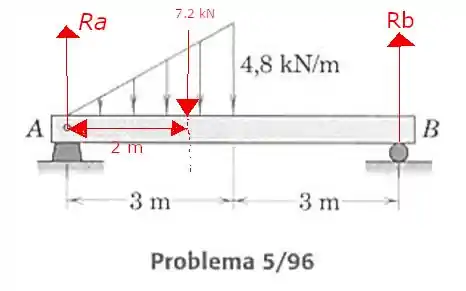
Passo 3

Agora se fizermos o somatório das forças nós vamos ter:

R a + R b - 7.2   k N = 0 → R a + R b = 7.2   k N

E agora o somatório dos momentos em A, considerando o sentido horário como o sentido positivo, nós teremos:

7.2 k N × 2 - R b × 6 = 0

R b × 6 = 14.4   k N → R b = 2.4   k N

Aplicando o valor de R b no somatório de forças nós teremos um R a igual a:

R a + 2.4 k N = 7.2   k N → R a = 4.8   k N

Resposta

R a = 4.8   k N

R b = 2.4   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

113- Uma viga está submetida ao carregamento variável mostrado. Calcule as reações nos apoios A e B.
108- A viga em balanço está submetida a uma carga distribuída parabólica, simétrica em relação ao meio da viga. Determine a força R a e o momento M a atuando na viga em A.
104- A viga está submetida a carga distribuída e ao momento mostrado. Se M for aumentado lentamente a partir de zero, em que valor M 0 o contato em B mudará da superfície inferior para a superior?
109- Determine a força e o momento de reação no apoio A da viga em balanço que está submetida a carga distribuída mostrada.
107- Determine as reações nos pontos A e B da viga submetida as cargas distribuídas uniforme e elíptica. Em qual superfície, inferior ou superior, atua a reação em A .