Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.6 - Ex. 98
98- Determine as reações em A e B para a viga carregada.
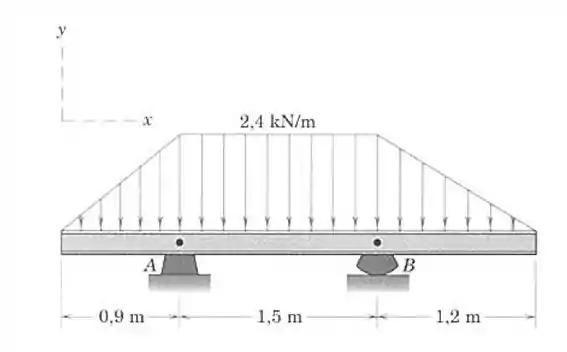
Passo 1
Esse trapézio pode ser dividido em três áreas, dois triângulos e um retângulo da seguinte forma:
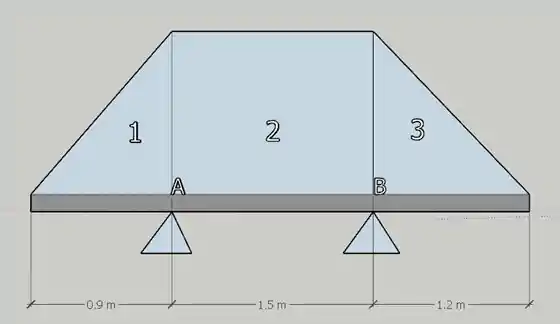
Onde a força resultando na área 1, será igual a sua área, que é igual a:
A força resultante na área 2 será sua área e será:
E a força resultante na área 3 será:
Passo 2
E as distâncias dessas forças estarão na coordenada horizontal do centroide dessas áreas:
Para a área 1:
Ou a do suporte A.
Para a área 2:
E para a área 3:
Logo poderemos substituir o carregamento da seguinte forma:
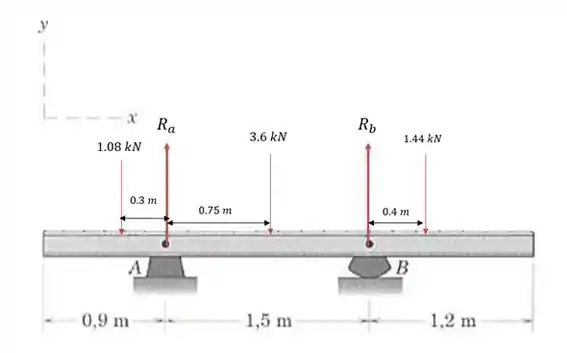
Passo 3
Como temos reações nos apoios A e B, podemos fazer o somatório das forças verticais iguais a zero:
Agora fazendo a somatória dos momentos em A igual a zero, adotando o sentido horário como positivo.
Logo será igual a:
Mesmo que o suporte A tenha resistência horizontal a carga não oferece força horizontal, logo um possível será igual a 0.